Functions
Unitaries

Unitary gates. More...

Functions

void compactUnitary (Qureg qureg, int targetQubit, Complex alpha, Complex beta)
 Apply a single-qubit unitary parameterised by two given complex scalars. More...
 
void controlledCompactUnitary (Qureg qureg, int controlQubit, int targetQubit, Complex alpha, Complex beta)
 Apply a controlled unitary (single control, single target) parameterised by two given complex scalars. More...
 
void controlledMultiQubitUnitary (Qureg qureg, int ctrl, int *targs, int numTargs, ComplexMatrixN u)
 Apply a general controlled multi-qubit unitary (including a global phase factor). More...
 
void controlledNot (Qureg qureg, int controlQubit, int targetQubit)
 Apply the controlled not (single control, single target) gate, also known as the c-X, c-sigma-X, c-Pauli-X and c-bit-flip gate. More...
 
void controlledPauliY (Qureg qureg, int controlQubit, int targetQubit)
 Apply the controlled pauliY (single control, single target) gate, also known as the c-Y and c-sigma-Y gate. More...
 
void controlledPhaseFlip (Qureg qureg, int idQubit1, int idQubit2)
 Apply the (two-qubit) controlled phase flip gate, also known as the controlled pauliZ gate. More...
 
void controlledPhaseShift (Qureg qureg, int idQubit1, int idQubit2, qreal angle)
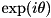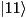 Introduce a phase factor $ \exp(i \theta) $ on state $ |11\rangle $ of qubits idQubit1 and idQubit2. More...
 
void controlledRotateAroundAxis (Qureg qureg, int controlQubit, int targetQubit, qreal angle, Vector axis)
 Applies a controlled rotation by a given angle around a given vector on the Bloch-sphere. More...
 
void controlledRotateX (Qureg qureg, int controlQubit, int targetQubit, qreal angle)
 Applies a controlled rotation by a given angle around the X-axis of the Bloch-sphere. More...
 
void controlledRotateY (Qureg qureg, int controlQubit, int targetQubit, qreal angle)
 Applies a controlled rotation by a given angle around the Y-axis of the Bloch-sphere. More...
 
void controlledRotateZ (Qureg qureg, int controlQubit, int targetQubit, qreal angle)
 Applies a controlled rotation by a given angle around the Z-axis of the Bloch-sphere. More...
 
void controlledTwoQubitUnitary (Qureg qureg, int controlQubit, int targetQubit1, int targetQubit2, ComplexMatrix4 u)
 Apply a general controlled two-qubit unitary (including a global phase factor). More...
 
void controlledUnitary (Qureg qureg, int controlQubit, int targetQubit, ComplexMatrix2 u)
 Apply a general controlled unitary (single control, single target), which can include a global phase factor. More...
 
void hadamard (Qureg qureg, int targetQubit)
 Apply the single-qubit Hadamard gate. More...
 
void multiControlledMultiQubitNot (Qureg qureg, int *ctrls, int numCtrls, int *targs, int numTargs)
 Apply a NOT (or Pauli X) gate with multiple control and target qubits. More...
 
void multiControlledMultiQubitUnitary (Qureg qureg, int *ctrls, int numCtrls, int *targs, int numTargs, ComplexMatrixN u)
 Apply a general multi-controlled multi-qubit unitary (including a global phase factor). More...
 
void multiControlledMultiRotatePauli (Qureg qureg, int *controlQubits, int numControls, int *targetQubits, enum pauliOpType *targetPaulis, int numTargets, qreal angle)
 Apply a multi-controlled multi-target multi-Pauli rotation, also known as a controlled Pauli gadget. More...
 
void multiControlledMultiRotateZ (Qureg qureg, int *controlQubits, int numControls, int *targetQubits, int numTargets, qreal angle)
 Apply a multi-controlled multi-target Z rotation, also known as a controlled phase gadget. More...
 
void multiControlledPhaseFlip (Qureg qureg, int *controlQubits, int numControlQubits)
 Apply the multiple-qubit controlled phase flip gate, also known as the multiple-qubit controlled pauliZ gate. More...
 
void multiControlledPhaseShift (Qureg qureg, int *controlQubits, int numControlQubits, qreal angle)
 Introduce a phase factor 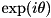$ \exp(i \theta) $ on state $ |1 \dots 1 \rangle $ of the passed qubits. More...
 
void multiControlledTwoQubitUnitary (Qureg qureg, int *controlQubits, int numControlQubits, int targetQubit1, int targetQubit2, ComplexMatrix4 u)
 Apply a general multi-controlled two-qubit unitary (including a global phase factor). More...
 
void multiControlledUnitary (Qureg qureg, int *controlQubits, int numControlQubits, int targetQubit, ComplexMatrix2 u)
 Apply a general multiple-control single-target unitary, which can include a global phase factor. More...
 
void multiQubitNot (Qureg qureg, int *targs, int numTargs)
 Apply a NOT (or Pauli X) gate with multiple target qubits, which has the same effect as (but is much faster than) applying each single-qubit NOT gate in turn. More...
 
void multiQubitUnitary (Qureg qureg, int *targs, int numTargs, ComplexMatrixN u)
 Apply a general multi-qubit unitary (including a global phase factor) with any number of target qubits. More...
 
void multiRotatePauli (Qureg qureg, int *targetQubits, enum pauliOpType *targetPaulis, int numTargets, qreal angle)
 Apply a multi-qubit multi-Pauli rotation, also known as a Pauli gadget, on a selected number of qubits. More...
 
void multiRotateZ (Qureg qureg, int *qubits, int numQubits, qreal angle)
 Apply a multi-qubit Z rotation, also known as a phase gadget, on a selected number of qubits. More...
 
void multiStateControlledUnitary (Qureg qureg, int *controlQubits, int *controlState, int numControlQubits, int targetQubit, ComplexMatrix2 u)
 Apply a general single-qubit unitary with multiple control qubits, conditioned upon a specific bit sequence. More...
 
void pauliX (Qureg qureg, int targetQubit)
 Apply the single-qubit Pauli-X (also known as the X, sigma-X, NOT or bit-flip) gate. More...
 
void pauliY (Qureg qureg, int targetQubit)
 Apply the single-qubit Pauli-Y (also known as the Y or sigma-Y) gate. More...
 
void pauliZ (Qureg qureg, int targetQubit)
 Apply the single-qubit Pauli-Z (also known as the Z, sigma-Z or phase-flip) gate. More...
 
void phaseShift (Qureg qureg, int targetQubit, qreal angle)
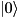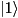 Shift the phase between $ |0\rangle $ and $ |1\rangle $ of a single qubit by a given angle. More...
 
void rotateAroundAxis (Qureg qureg, int rotQubit, qreal angle, Vector axis)
 Rotate a single qubit by a given angle around a given Vector on the Bloch-sphere. More...
 
void rotateX (Qureg qureg, int rotQubit, qreal angle)
 Rotate a single qubit by a given angle around the X-axis of the Bloch-sphere. More...
 
void rotateY (Qureg qureg, int rotQubit, qreal angle)
 Rotate a single qubit by a given angle around the Y-axis of the Bloch-sphere. More...
 
void rotateZ (Qureg qureg, int rotQubit, qreal angle)
 Rotate a single qubit by a given angle around the Z-axis of the Bloch-sphere (also known as a phase shift gate). More...
 
void sGate (Qureg qureg, int targetQubit)
 Apply the single-qubit S gate. More...
 
void sqrtSwapGate (Qureg qureg, int qb1, int qb2)
 Performs a sqrt SWAP gate between qubit1 and qubit2. More...
 
void swapGate (Qureg qureg, int qubit1, int qubit2)
 Performs a SWAP gate between qubit1 and qubit2. More...
 
void tGate (Qureg qureg, int targetQubit)
 Apply the single-qubit T gate. More...
 
void twoQubitUnitary (Qureg qureg, int targetQubit1, int targetQubit2, ComplexMatrix4 u)
 Apply a general two-qubit unitary (including a global phase factor). More...
 
void unitary (Qureg qureg, int targetQubit, ComplexMatrix2 u)
 Apply a general single-qubit unitary (including a global phase factor). More...
 

Detailed Description

Unitary gates.

Function Documentation

◆ compactUnitary()

void compactUnitary ( Qureg  qureg,
int  targetQubit,
Complex  alpha,
Complex  beta 
)

Apply a single-qubit unitary parameterised by two given complex scalars.

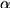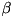Given valid complex numbers $\alpha$ and $\beta$, applies the unitary

\[ U = \begin{pmatrix} \alpha & -\beta^* \\ \beta & \alpha^* \end{pmatrix} \]

which is general up to a global phase factor.
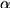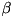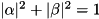Valid $\alpha$, $\beta$ satisfy $|\alpha|^2 + |\beta|^2 = 1$.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {target}; \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {U}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]targetQubitqubit to operate on
[in]alphacomplex unitary parameter (row 1, column 1)
[in]betacomplex unitary parameter (row 2, column 1)
Exceptions
invalidQuESTInputError()
  • if targetQubit is outside [0, qureg.numQubitsRepresented)
  • if alpha, beta don't satisfy |alpha|^2 + |beta|^2 = 1
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 404 of file QuEST.c.

404  {
405  validateTarget(qureg, targetQubit, __func__);
406  validateUnitaryComplexPair(alpha, beta, __func__);
407 
408  statevec_compactUnitary(qureg, targetQubit, alpha, beta);
409  if (qureg.isDensityMatrix) {
410  int shift = qureg.numQubitsRepresented;
411  statevec_compactUnitary(qureg, targetQubit+shift, getConjugateScalar(alpha), getConjugateScalar(beta));
412  }
413 
414  qasm_recordCompactUnitary(qureg, alpha, beta, targetQubit);
415 }

References getConjugateScalar(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordCompactUnitary(), statevec_compactUnitary(), validateTarget(), and validateUnitaryComplexPair().

Referenced by TEST_CASE().

◆ controlledCompactUnitary()

void controlledCompactUnitary ( Qureg  qureg,
int  controlQubit,
int  targetQubit,
Complex  alpha,
Complex  beta 
)

Apply a controlled unitary (single control, single target) parameterised by two given complex scalars.

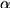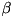Given valid complex numbers $\alpha$ and $\beta$, applies the two-qubit unitary

\[ \begin{pmatrix} 1 \\ & 1 \\ & & \alpha & -\beta^* \\ & & \beta & \alpha^* \end{pmatrix} \]

to the control and target qubits. Valid 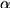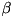$\alpha$, $\beta$ satisfy 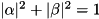$|\alpha|^2 + |\beta|^2 = 1$. The target unitary is general up to a global phase factor.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {control}; \node[draw=none] at (-3.5, 0) {target}; \draw (-2, 2) -- (2, 2); \draw[fill=black] (0, 2) circle (.2); \draw (0, 2) -- (0, 1); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {$U_{\alpha, \beta}$}; \end{tikzpicture} \]

See also


Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitapply the target unitary if this qubit has value 1
[in]targetQubitqubit on which to apply the target unitary
[in]alphacomplex unitary parameter (row 1, column 1)
[in]betacomplex unitary parameter (row 2, column 1)
Exceptions
invalidQuESTInputError()
  • if either controlQubit or targetQubit are outside [0, qureg.numQubitsRepresented)
  • if controlQubit and targetQubit are equal
  • if alpha, beta don't satisfy |alpha|^2 + |beta|^2 = 1
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 417 of file QuEST.c.

417  {
418  validateControlTarget(qureg, controlQubit, targetQubit, __func__);
419  validateUnitaryComplexPair(alpha, beta, __func__);
420 
421  statevec_controlledCompactUnitary(qureg, controlQubit, targetQubit, alpha, beta);
422  if (qureg.isDensityMatrix) {
423  int shift = qureg.numQubitsRepresented;
424  statevec_controlledCompactUnitary(qureg,
425  controlQubit+shift, targetQubit+shift,
426  getConjugateScalar(alpha), getConjugateScalar(beta));
427  }
428 
429  qasm_recordControlledCompactUnitary(qureg, alpha, beta, controlQubit, targetQubit);
430 }

References getConjugateScalar(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordControlledCompactUnitary(), statevec_controlledCompactUnitary(), validateControlTarget(), and validateUnitaryComplexPair().

Referenced by TEST_CASE().

◆ controlledMultiQubitUnitary()

void controlledMultiQubitUnitary ( Qureg  qureg,
int  ctrl,
int *  targs,
int  numTargs,
ComplexMatrixN  u 
)

Apply a general controlled multi-qubit unitary (including a global phase factor).

One control and any number of target qubits can be specified. This effects the many-qubit unitary

\[ \begin{pmatrix} 1 \\ & 1 \\\ & & 1 \\ & & & 1 \\ & & & & u_{00} & u_{01} & \dots \\ & & & & u_{10} & u_{11} & \dots \\ & & & & \vdots & \vdots & \ddots \end{pmatrix} \]

on the control and target qubits.

The target qubits in targs are treated as ordered least significant to most significant in u.

The passed ComplexMatrix must be unitary and be a compatible size with the specified number of target qubits, otherwise an error is thrown.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 1) {targets}; \node[draw=none] at (-3.5, 4) {control}; \draw (-2, 4) -- (2, 4); \draw[fill=black] (0, 4) circle (.2); \draw(0, 4) -- (0, 3); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-2,2) -- (-1, 2); \draw (1, 2) -- (2, 2); \draw (-1,-1)--(-1,3)--(1,3)--(1,-1); \node[draw=none] at (0, 1) {U}; \node[draw=none] at (0, -1) {$\vdots$}; \end{tikzpicture} \]

Note that in multithreaded mode, each thread will clone 2^numTargs amplitudes, and store these in the runtime stack. Using t threads, the total memory overhead of this function is t*2^numTargs. For many targets (e.g. 16 qubits), this may cause a stack-overflow / seg-fault (e.g. on a 1 MiB stack).

Note too that in distributed mode, this routine requires that each node contains at least 2^numTargs amplitudes. This means an q-qubit register (state vector or density matrix) can be distributed by at most 2^q / 2^numTargs nodes.

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]ctrlthe control qubit
[in]targsa list of the target qubits, ordered least to most significant
[in]numTargsthe number of target qubits
[in]uunitary matrix to apply
Exceptions
invalidQuESTInputError()
  • if ctrl or any index in targs is outside of [0, qureg.numQubitsRepresented)
  • if targs are not unique
  • if targs contains ctrl
  • if matrix u is not unitary
  • if a node cannot fit the required number of target amplitudes in distributed mode
Author
Tyson Jones

Definition at line 313 of file QuEST.c.

313  {
314  validateMultiControlsMultiTargets(qureg, (int[]) {ctrl}, 1, targs, numTargs, __func__);
315  validateMultiQubitUnitaryMatrix(qureg, u, numTargs, __func__);
316 
317  statevec_controlledMultiQubitUnitary(qureg, ctrl, targs, numTargs, u);
318  if (qureg.isDensityMatrix) {
319  int shift = qureg.numQubitsRepresented;
320  shiftIndices(targs, numTargs, shift);
321  setConjugateMatrixN(u);
322  statevec_controlledMultiQubitUnitary(qureg, ctrl+shift, targs, numTargs, u);
323  shiftIndices(targs, numTargs, -shift);
324  setConjugateMatrixN(u);
325  }
326 
327  qasm_recordComment(qureg, "Here, an undisclosed controlled multi-qubit unitary was applied.");
328 }

References Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordComment(), setConjugateMatrixN(), shiftIndices(), statevec_controlledMultiQubitUnitary(), validateMultiControlsMultiTargets(), and validateMultiQubitUnitaryMatrix().

Referenced by TEST_CASE().

◆ controlledNot()

void controlledNot ( Qureg  qureg,
int  controlQubit,
int  targetQubit 
)

Apply the controlled not (single control, single target) gate, also known as the c-X, c-sigma-X, c-Pauli-X and c-bit-flip gate.

This applies pauliX to the target qubit if the control qubit has value 1. This effects the two-qubit unitary

\[ \begin{pmatrix} 1 \\ & 1 \\\ & & & 1 \\ & & 1 \end{pmatrix} \]

on the control and target qubits.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {control}; \node[draw=none] at (-3.5, 0) {target}; \draw (-2, 2) -- (2, 2); \draw[fill=black] (0, 2) circle (.2); \draw (0, 2) -- (0, -.5); \draw (-2,0) -- (2, 0); \draw (0, 0) circle (.5); \end{tikzpicture} \]

See also
Parameters
[in,out]quregthe state-vector or density matrix to modify
[in]controlQubitnots the target if this qubit is 1
[in]targetQubitqubit to not
Exceptions
invalidQuESTInputError()
  • if either controlQubit or targetQubit are outside [0, qureg.numQubitsRepresented)
  • if controlQubit and targetQubit are equal
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 524 of file QuEST.c.

524  {
525  validateControlTarget(qureg, controlQubit, targetQubit, __func__);
526 
527  statevec_controlledNot(qureg, controlQubit, targetQubit);
528  if (qureg.isDensityMatrix) {
529  int shift = qureg.numQubitsRepresented;
530  statevec_controlledNot(qureg, controlQubit+shift, targetQubit+shift);
531  }
532 
533  qasm_recordControlledGate(qureg, GATE_SIGMA_X, controlQubit, targetQubit);
534 }

References GATE_SIGMA_X, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordControlledGate(), statevec_controlledNot(), and validateControlTarget().

Referenced by TEST_CASE().

◆ controlledPauliY()

void controlledPauliY ( Qureg  qureg,
int  controlQubit,
int  targetQubit 
)

Apply the controlled pauliY (single control, single target) gate, also known as the c-Y and c-sigma-Y gate.

This applies pauliY to the target qubit if the control qubit has value 1. This effects the two-qubit unitary

\[ \begin{pmatrix} 1 \\ & 1 \\\ & & & -i \\ & & i \end{pmatrix} \]

on the control and target qubits.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {control}; \node[draw=none] at (-3.5, 0) {target}; \draw (-2, 2) -- (2, 2); \draw[fill=black] (0, 2) circle (.2); \draw (0, 2) -- (0, 1); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {Y}; \end{tikzpicture} \]

Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitapplies pauliY to the target if this qubit is 1
[in]targetQubitqubit to not
Exceptions
invalidQuESTInputError()
  • if either controlQubit or targetQubit are outside [0, qureg.numQubitsRepresented)
  • if controlQubit and targetQubit are equal
Author
Tyson Jones
Ania Brown (debug)

Definition at line 563 of file QuEST.c.

563  {
564  validateControlTarget(qureg, controlQubit, targetQubit, __func__);
565 
566  statevec_controlledPauliY(qureg, controlQubit, targetQubit);
567  if (qureg.isDensityMatrix) {
568  int shift = qureg.numQubitsRepresented;
569  statevec_controlledPauliYConj(qureg, controlQubit+shift, targetQubit+shift);
570  }
571 
572  qasm_recordControlledGate(qureg, GATE_SIGMA_Y, controlQubit, targetQubit);
573 }

References GATE_SIGMA_Y, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordControlledGate(), statevec_controlledPauliY(), statevec_controlledPauliYConj(), and validateControlTarget().

Referenced by TEST_CASE().

◆ controlledPhaseFlip()

void controlledPhaseFlip ( Qureg  qureg,
int  idQubit1,
int  idQubit2 
)

Apply the (two-qubit) controlled phase flip gate, also known as the controlled pauliZ gate.

For each state, if both input qubits have value one, multiply the amplitude of that state by -1. This applies the two-qubit unitary:

\[ \begin{pmatrix} 1 \\ & 1 \\\ & & 1 \\ & & & -1 \end{pmatrix} \]

with circuit diagram:

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {idQubit1}; \node[draw=none] at (-3.5, 0) {idQubit2}; \draw (-2, 2) -- (2, 2); \draw[fill=black] (0, 2) circle (.2); \draw (0, 2) -- (0, 0); \draw (-2,0) -- (2, 0); \draw[fill=black] (0, 0) circle (.2); \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]idQubit1,idQubit2qubits to operate upon
Exceptions
invalidQuESTInputError()
  • if idQubit1 or idQubit2 are outside [0, qureg.numQubitsRepresented)
  • if idQubit1 and idQubit2 are equal
Author
Tyson Jones

Definition at line 575 of file QuEST.c.

575  {
576  validateControlTarget(qureg, idQubit1, idQubit2, __func__);
577 
578  statevec_controlledPhaseFlip(qureg, idQubit1, idQubit2);
579  if (qureg.isDensityMatrix) {
580  int shift = qureg.numQubitsRepresented;
581  statevec_controlledPhaseFlip(qureg, idQubit1+shift, idQubit2+shift);
582  }
583 
584  qasm_recordControlledGate(qureg, GATE_SIGMA_Z, idQubit1, idQubit2);
585 }

References GATE_SIGMA_Z, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordControlledGate(), statevec_controlledPhaseFlip(), and validateControlTarget().

Referenced by TEST_CASE().

◆ controlledPhaseShift()

void controlledPhaseShift ( Qureg  qureg,
int  idQubit1,
int  idQubit2,
qreal  angle 
)

Introduce a phase factor 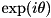$ \exp(i \theta) $ on state 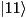$ |11\rangle $ of qubits idQubit1 and idQubit2.

For angle 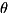$\theta$, this effects the unitary

\[ \begin{pmatrix} 1 & & & \\ & 1 & & \\ & & 1 & \\ & & & \exp(i \theta) \end{pmatrix} \]

on idQubit1 and idQubit2.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {qubit1}; \node[draw=none] at (-3.5, 0) {qubit2}; \draw (-2, 2) -- (2, 2); \draw[fill=black] (0, 2) circle (.2); \draw (0, 2) -- (0, 1); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {$R_\theta$}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]idQubit1first qubit in the state to phase shift
[in]idQubit2second qubit in the state to phase shift
[in]angleamount by which to shift the phase in radians
Exceptions
invalidQuESTInputError()
  • if idQubit1 or idQubit2 are outside [0, qureg.numQubitsRepresented)
  • if idQubit1 and idQubit2 are equal
Author
Tyson Jones

Definition at line 498 of file QuEST.c.

498  {
499  validateControlTarget(qureg, idQubit1, idQubit2, __func__);
500 
501  statevec_controlledPhaseShift(qureg, idQubit1, idQubit2, angle);
502  if (qureg.isDensityMatrix) {
503  int shift = qureg.numQubitsRepresented;
504  statevec_controlledPhaseShift(qureg, idQubit1+shift, idQubit2+shift, -angle);
505  }
506 
507  qasm_recordControlledParamGate(qureg, GATE_PHASE_SHIFT, idQubit1, idQubit2, angle);
508 }

References GATE_PHASE_SHIFT, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordControlledParamGate(), statevec_controlledPhaseShift(), and validateControlTarget().

Referenced by TEST_CASE().

◆ controlledRotateAroundAxis()

void controlledRotateAroundAxis ( Qureg  qureg,
int  controlQubit,
int  targetQubit,
qreal  angle,
Vector  axis 
)

Applies a controlled rotation by a given angle around a given vector on the Bloch-sphere.


The vector must not be zero (else an error is thrown), but needn't be unit magnitude.

For angle 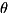$\theta$ and axis vector 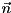$\vec{n}$, applies 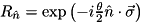$R_{\hat{n}} = \exp \left(- i \frac{\theta}{2} \hat{n} \cdot \vec{\sigma} \right) $ to states where the target qubit is 1 ( 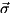$\vec{\sigma}$ is the vector of Pauli matrices).

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {control}; \node[draw=none] at (-3.5, 0) {target}; \draw (-2, 2) -- (2, 2); \draw[fill=black] (0, 2) circle (.2); \draw (0, 2) -- (0, 1); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {$R_{\hat{n}}(\theta)$}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitqubit with value 1 in the rotated states
[in]targetQubitqubit to rotate
[in]angleangle by which to rotate in radians
[in]axisvector around which to rotate (can be non-unit; will be normalised)
Exceptions
invalidQuESTInputError()
  • if either controlQubit or targetQubit are outside [0, qureg.numQubitsRepresented)
  • if controlQubit and targetQubit are equal
  • if axis is the zero vector
Author
Tyson Jones

Definition at line 614 of file QuEST.c.

614  {
615  validateControlTarget(qureg, controlQubit, targetQubit, __func__);
616  validateVector(axis, __func__);
617 
618  statevec_controlledRotateAroundAxis(qureg, controlQubit, targetQubit, angle, axis);
619  if (qureg.isDensityMatrix) {
620  int shift = qureg.numQubitsRepresented;
621  statevec_controlledRotateAroundAxisConj(qureg, controlQubit+shift, targetQubit+shift, angle, axis);
622  }
623 
624  qasm_recordControlledAxisRotation(qureg, angle, axis, controlQubit, targetQubit);
625 }

References Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordControlledAxisRotation(), statevec_controlledRotateAroundAxis(), statevec_controlledRotateAroundAxisConj(), validateControlTarget(), and validateVector().

Referenced by TEST_CASE().

◆ controlledRotateX()

void controlledRotateX ( Qureg  qureg,
int  controlQubit,
int  targetQubit,
qreal  angle 
)

Applies a controlled rotation by a given angle around the X-axis of the Bloch-sphere.

The target qubit is rotated in states where the control qubit has value 1.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {control}; \node[draw=none] at (-3.5, 0) {target}; \draw (-2, 2) -- (2, 2); \draw[fill=black] (0, 2) circle (.2); \draw (0, 2) -- (0, 1); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {$R_x(\theta)$}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitqubit which has value 1 in the rotated states
[in]targetQubitqubit to rotate
[in]angleangle by which to rotate the target qubit in radians
Exceptions
invalidQuESTInputError()
  • if either controlQubit or targetQubit are outside [0, qureg.numQubitsRepresented)
  • if controlQubit and targetQubit are equal
Author
Tyson Jones

Definition at line 220 of file QuEST.c.

220  {
221  validateControlTarget(qureg, controlQubit, targetQubit, __func__);
222 
223  statevec_controlledRotateX(qureg, controlQubit, targetQubit, angle);
224  if (qureg.isDensityMatrix) {
225  int shift = qureg.numQubitsRepresented;
226  statevec_controlledRotateX(qureg, controlQubit+shift, targetQubit+shift, -angle);
227  }
228 
229  qasm_recordControlledParamGate(qureg, GATE_ROTATE_X, controlQubit, targetQubit, angle);
230 }

References GATE_ROTATE_X, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordControlledParamGate(), statevec_controlledRotateX(), and validateControlTarget().

Referenced by TEST_CASE().

◆ controlledRotateY()

void controlledRotateY ( Qureg  qureg,
int  controlQubit,
int  targetQubit,
qreal  angle 
)

Applies a controlled rotation by a given angle around the Y-axis of the Bloch-sphere.

The target qubit is rotated in states where the control qubit has value 1.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {control}; \node[draw=none] at (-3.5, 0) {target}; \draw (-2, 2) -- (2, 2); \draw[fill=black] (0, 2) circle (.2); \draw (0, 2) -- (0, 1); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {$R_y(\theta)$}; \end{tikzpicture} \]

Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitqubit which has value 1 in the rotated states
[in]targetQubitqubit to rotate
[in]angleangle by which to rotate the target qubit in radians
Exceptions
invalidQuESTInputError()
  • if either controlQubit or targetQubit are outside [0, qureg.numQubitsRepresented)
  • if controlQubit and targetQubit are equal
Author
Tyson Jones

Definition at line 232 of file QuEST.c.

232  {
233  validateControlTarget(qureg, controlQubit, targetQubit, __func__);
234 
235  statevec_controlledRotateY(qureg, controlQubit, targetQubit, angle);
236  if (qureg.isDensityMatrix) {
237  int shift = qureg.numQubitsRepresented;
238  statevec_controlledRotateY(qureg, controlQubit+shift, targetQubit+shift, angle); // rotateY is real
239  }
240 
241  qasm_recordControlledParamGate(qureg, GATE_ROTATE_Y, controlQubit, targetQubit, angle);
242 }

References GATE_ROTATE_Y, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordControlledParamGate(), statevec_controlledRotateY(), and validateControlTarget().

Referenced by TEST_CASE().

◆ controlledRotateZ()

void controlledRotateZ ( Qureg  qureg,
int  controlQubit,
int  targetQubit,
qreal  angle 
)

Applies a controlled rotation by a given angle around the Z-axis of the Bloch-sphere.

The target qubit is rotated in states where the control qubit has value 1.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {control}; \node[draw=none] at (-3.5, 0) {target}; \draw (-2, 2) -- (2, 2); \draw[fill=black] (0, 2) circle (.2); \draw (0, 2) -- (0, 1); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {$R_z(\theta)$}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitqubit which has value 1 in the rotated states
[in]targetQubitqubit to rotate
[in]angleangle by which to rotate the target qubit in radians
Exceptions
invalidQuESTInputError()
  • if either controlQubit or targetQubit are outside [0, qureg.numQubitsRepresented)
  • if controlQubit and targetQubit are equal
Author
Tyson Jones

Definition at line 244 of file QuEST.c.

244  {
245  validateControlTarget(qureg, controlQubit, targetQubit, __func__);
246 
247  statevec_controlledRotateZ(qureg, controlQubit, targetQubit, angle);
248  if (qureg.isDensityMatrix) {
249  int shift = qureg.numQubitsRepresented;
250  statevec_controlledRotateZ(qureg, controlQubit+shift, targetQubit+shift, -angle);
251  }
252 
253  qasm_recordControlledParamGate(qureg, GATE_ROTATE_Z, controlQubit, targetQubit, angle);
254 }

References GATE_ROTATE_Z, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordControlledParamGate(), statevec_controlledRotateZ(), and validateControlTarget().

Referenced by TEST_CASE().

◆ controlledTwoQubitUnitary()

void controlledTwoQubitUnitary ( Qureg  qureg,
int  controlQubit,
int  targetQubit1,
int  targetQubit2,
ComplexMatrix4  u 
)

Apply a general controlled two-qubit unitary (including a global phase factor).

The given unitary is applied to the target amplitudes where the control qubit has value 1. This effects the many-qubit unitary

\[ \begin{pmatrix} 1 \\ & 1 \\ & & 1 \\ & & & 1 \\ & & & & u_{00} & u_{01} & u_{02} & u_{03} \\ & & & & u_{10} & u_{11} & u_{12} & u_{13} \\ & & & & u_{20} & u_{21} & u_{22} & u_{23} \\ & & & & u_{30} & u_{31} & u_{32} & u_{33} \end{pmatrix} \]

on the control and target qubits.

targetQubit1 is treated as the least significant qubit in u, such that a row in u is dotted with the vector 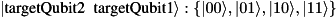$ |\text{targetQubit2} \;\; \text{targetQubit1}\rangle : \{ |00\rangle, |01\rangle, |10\rangle, |11\rangle \} $

The passed 4x4 ComplexMatrix must be unitary, otherwise an error is thrown.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {target1}; \node[draw=none] at (-3.5, 2) {target2}; \node[draw=none] at (-3.5, 4) {control}; \draw (-2, 4) -- (2, 4); \draw[fill=black] (0, 4) circle (.2); \draw(0, 4) -- (0, 3); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-2,2) -- (-1, 2); \draw (1, 2) -- (2, 2); \draw (-1,-1)--(-1,3)--(1,3)--(1,-1)--cycle; \node[draw=none] at (0, 1) {U}; \end{tikzpicture} \]

Note that in distributed mode, this routine requires that each node contains at least 4 amplitudes. This means an q-qubit register (state vector or density matrix) can be distributed by at most 2^q/4 nodes.

See also


Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitthe control qubit which must be in state 1 to effect the given unitary
[in]targetQubit1first qubit to operate on, treated as least significant in u
[in]targetQubit2second qubit to operate on, treated as most significant in u
[in]uunitary matrix to apply
Exceptions
invalidQuESTInputError()
  • if controlQubit, targetQubit1 or targetQubit2 are outside [0, qureg.numQubitsRepresented)
  • if any of controlQubit, targetQubit1 and targetQubit2 are equal
  • if matrix u is not unitary
    • if each node cannot fit 4 amplitudes in distributed mode.
Author
Tyson Jones

Definition at line 269 of file QuEST.c.

269  {
270  validateMultiControlsMultiTargets(qureg, (int[]) {controlQubit}, 1, (int[]) {targetQubit1, targetQubit2}, 2, __func__);
271  validateTwoQubitUnitaryMatrix(qureg, u, __func__);
272 
273  statevec_controlledTwoQubitUnitary(qureg, controlQubit, targetQubit1, targetQubit2, u);
274  if (qureg.isDensityMatrix) {
275  int shift = qureg.numQubitsRepresented;
276  statevec_controlledTwoQubitUnitary(qureg, controlQubit+shift, targetQubit1+shift, targetQubit2+shift, getConjugateMatrix4(u));
277  }
278 
279  qasm_recordComment(qureg, "Here, an undisclosed controlled 2-qubit unitary was applied.");
280 }

References getConjugateMatrix4(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordComment(), statevec_controlledTwoQubitUnitary(), validateMultiControlsMultiTargets(), and validateTwoQubitUnitaryMatrix().

Referenced by TEST_CASE().

◆ controlledUnitary()

void controlledUnitary ( Qureg  qureg,
int  controlQubit,
int  targetQubit,
ComplexMatrix2  u 
)

Apply a general controlled unitary (single control, single target), which can include a global phase factor.

The given unitary is applied to the target qubit if the control qubit has value 1, effecting the two-qubit unitary

\[ \begin{pmatrix} 1 \\ & 1 \\ & & u_{00} & u_{01}\\ & & u_{10} & u_{11} \end{pmatrix} \]

on the control and target qubits.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {control}; \node[draw=none] at (-3.5, 0) {target}; \draw (-2, 2) -- (2, 2); \draw[fill=black] (0, 2) circle (.2); \draw (0, 2) -- (0, 1); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {U}; \end{tikzpicture} \]

See also


Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitapply unitary if this qubit is 1
[in]targetQubitqubit to operate on
[in]usingle-qubit unitary matrix to apply
Exceptions
invalidQuESTInputError()
  • if either controlQubit or targetQubit are outside [0, qureg.numQubitsRepresented)
  • if controlQubit and targetQubit are equal
  • if u is not unitary
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 360 of file QuEST.c.

360  {
361  validateControlTarget(qureg, controlQubit, targetQubit, __func__);
362  validateOneQubitUnitaryMatrix(u, __func__);
363 
364  statevec_controlledUnitary(qureg, controlQubit, targetQubit, u);
365  if (qureg.isDensityMatrix) {
366  int shift = qureg.numQubitsRepresented;
367  statevec_controlledUnitary(qureg, controlQubit+shift, targetQubit+shift, getConjugateMatrix2(u));
368  }
369 
370  qasm_recordControlledUnitary(qureg, u, controlQubit, targetQubit);
371 }

References getConjugateMatrix2(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordControlledUnitary(), statevec_controlledUnitary(), validateControlTarget(), and validateOneQubitUnitaryMatrix().

Referenced by TEST_CASE().

◆ hadamard()

void hadamard ( Qureg  qureg,
int  targetQubit 
)

Apply the single-qubit Hadamard gate.

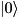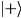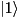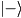This takes $|0\rangle$ to $|+\rangle$ and $|1\rangle$ to $|-\rangle$, and is equivalent to a rotation of 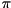$\pi$ around the x-axis then 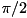$\pi/2$ about the y-axis on the Bloch-sphere. I.e.

\[ \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \]

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {target}; \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {H}; \end{tikzpicture} \]

Parameters
[in,out]quregobject representing the set of all qubits
[in]targetQubitqubit to operate on
Exceptions
invalidQuESTInputError()
  • if targetQubit is outside [0, qureg.numQubitsRepresented)
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 176 of file QuEST.c.

176  {
177  validateTarget(qureg, targetQubit, __func__);
178 
179  statevec_hadamard(qureg, targetQubit);
180  if (qureg.isDensityMatrix) {
181  statevec_hadamard(qureg, targetQubit+qureg.numQubitsRepresented);
182  }
183 
184  qasm_recordGate(qureg, GATE_HADAMARD, targetQubit);
185 }

References GATE_HADAMARD, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordGate(), statevec_hadamard(), and validateTarget().

Referenced by TEST_CASE().

◆ multiControlledMultiQubitNot()

void multiControlledMultiQubitNot ( Qureg  qureg,
int *  ctrls,
int  numCtrls,
int *  targs,
int  numTargs 
)

Apply a NOT (or Pauli X) gate with multiple control and target qubits.

This applies pauliX to qubits targs on every basis state for which the control qubits ctrls are all in the 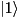$|1\rangle$ state. The ordering within each of ctrls and targs has no effect on the operation.

This function is equivalent, but significantly faster (approximately numTargs times) than applying controlled NOTs on each qubit in targs in turn, since:

\[ C_{a, \,b, \,\dots}( X_c \otimes X_d \otimes \dots ) \equiv C_{a, \,b, \,\dots}( X_c) \; \otimes \; C_{a, \,b, \,\dots}(X_d) \; \otimes \; \dots \]

The effected unitary, if targs and ctrls happened to be contiguous, has matrix:

\[ \begin{pmatrix} 1 \\ & 1 \\\ & & \ddots \\ & & & & & & {{\scriptstyle\cdot}^{{\scriptstyle\cdot}^{{\scriptstyle\cdot}}}} \\ & & & & & 1 & \\ & & & & 1 & & \\ & & & {{\scriptstyle\cdot}^{{\scriptstyle\cdot}^{{\scriptstyle\cdot}}}} & & & \end{pmatrix} \]

and circuit diagram:

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 1) {targets}; \node[draw=none] at (-3.5, 5) {controls}; \node[draw=none] at (0, 8) {$\vdots$}; \draw (0, 7) -- (0, 6); \draw (-2, 6) -- (2, 6); \draw[fill=black] (0, 6) circle (.2); \draw (0, 6) -- (0, 4); \draw (-2, 4) -- (2, 4); \draw[fill=black] (0, 4) circle (.2); \draw(0, 4) -- (0, -1); \draw (-2,2) -- (2, 2); \draw (0, 2) circle (.4); \draw (-2,0) -- (2, 0); \draw (0, 0) circle (.4); \node[draw=none] at (0, -1.5) {$\vdots$}; \end{tikzpicture} \]

In distributed mode, this operation requires at most a single round of pair-wise communication between nodes, and hence is as efficient as pauliX().

See also
Parameters
[in,out]qurega state-vector or density matrix to modify
[in]ctrlsa list of the control qubit indices
[in]numCtrlsthe length of list ctrls
[in]targsa list of the qubits to be targeted by the X gates
[in]numTargsthe length of list targs
Exceptions
invalidQuESTInputError()
  • if any qubit in ctrls and targs is invalid, i.e. outside [0, qureg.numQubitsRepresented)
  • if ctrls or targs contain any repetitions
  • if any qubit in ctrls is also in targs (and vice versa)
  • if numTargs < 1
  • if numCtrls < 1 (use multiQubitNot() for no controls)
segmentation-fault
  • if ctrls contains fewer elements than numCtrls
  • if targs contains fewer elements than numTargs
Author
Tyson Jones

Definition at line 549 of file QuEST.c.

549  {
550  validateMultiControlsMultiTargets(qureg, ctrls, numCtrls, targs, numTargs, __func__);
551 
552  long long int ctrlMask = getQubitBitMask(ctrls, numCtrls);
553  long long int targMask = getQubitBitMask(targs, numTargs);
554  statevec_multiControlledMultiQubitNot(qureg, ctrlMask, targMask);
555  if (qureg.isDensityMatrix) {
556  int shift = qureg.numQubitsRepresented;
557  statevec_multiControlledMultiQubitNot(qureg, ctrlMask<<shift, targMask<<shift);
558  }
559 
560  qasm_recordMultiControlledMultiQubitNot(qureg, ctrls, numCtrls, targs, numTargs);
561 }

References getQubitBitMask(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordMultiControlledMultiQubitNot(), statevec_multiControlledMultiQubitNot(), and validateMultiControlsMultiTargets().

Referenced by TEST_CASE().

◆ multiControlledMultiQubitUnitary()

void multiControlledMultiQubitUnitary ( Qureg  qureg,
int *  ctrls,
int  numCtrls,
int *  targs,
int  numTargs,
ComplexMatrixN  u 
)

Apply a general multi-controlled multi-qubit unitary (including a global phase factor).

Any number of control and target qubits can be specified. This effects the many-qubit unitary

\[ \begin{pmatrix} 1 \\ & 1 \\\ & & \ddots \\ & & & u_{00} & u_{01} & \dots \\ & & & u_{10} & u_{11} & \dots \\ & & & \vdots & \vdots & \ddots \end{pmatrix} \]

on the control and target qubits.

The target qubits in targs are treated as ordered least significant to most significant in u.

The passed ComplexMatrixN must be unitary and be a compatible size with the specified number of target qubits, otherwise an error is thrown.

To left-multiply a non-unitary ComplexMatrixN, including control qubits, use applyMultiControlledMatrixN()

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 1) {targets}; \node[draw=none] at (-3.5, 5) {controls}; \node[draw=none] at (0, 8) {$\vdots$}; \draw (0, 7) -- (0, 6); \draw (-2, 6) -- (2, 6); \draw[fill=black] (0, 6) circle (.2); \draw (0, 6) -- (0, 4); \draw (-2, 4) -- (2, 4); \draw[fill=black] (0, 4) circle (.2); \draw(0, 4) -- (0, 3); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-2,2) -- (-1, 2); \draw (1, 2) -- (2, 2); \draw (-1,-1)--(-1,3)--(1,3)--(1,-1); \node[draw=none] at (0, 1) {U}; \node[draw=none] at (0, -1) {$\vdots$}; \end{tikzpicture} \]

Note that in multithreaded mode, each thread will clone 2^numTargs amplitudes, and store these in the runtime stack. Using t threads, the total memory overhead of this function is t*2^numTargs. For many targets (e.g. 16 qubits), this may cause a stack-overflow / seg-fault (e.g. on a 1 MiB stack).

Note that in distributed mode, this routine requires that each node contains at least 2^numTargs amplitudes. This means an q-qubit register (state vector or density matrix) can be distributed by at most 2^q / 2^numTargs nodes.

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]ctrlsa list of the control qubits
[in]numCtrlsthe number of control qubits
[in]targsa list of the target qubits, ordered least to most significant
[in]numTargsthe number of target qubits
[in]uunitary matrix to apply
Exceptions
invalidQuESTInputError()
  • if any qubit in ctrls and targs is invalid, i.e. outside [0, qureg.numQubitsRepresented)
  • if ctrls or targs contain any repetitions
  • if any qubit in ctrls is also in targs (and vice versa)
  • if numTargs < 1
  • if numCtrls < 1 (use multiQubitUnitary() for no controls)
  • if matrix u is not unitary
  • if a node cannot fit the required number of target amplitudes in distributed mode
segmentation-fault
  • if ctrls contains fewer elements than numCtrls
  • if targs contains fewer elements than numTargs
Author
Tyson Jones

Definition at line 330 of file QuEST.c.

330  {
331  validateMultiControlsMultiTargets(qureg, ctrls, numCtrls, targs, numTargs, __func__);
332  validateMultiQubitUnitaryMatrix(qureg, u, numTargs, __func__);
333 
334  long long int ctrlMask = getQubitBitMask(ctrls, numCtrls);
335  statevec_multiControlledMultiQubitUnitary(qureg, ctrlMask, targs, numTargs, u);
336  if (qureg.isDensityMatrix) {
337  int shift = qureg.numQubitsRepresented;
338  shiftIndices(targs, numTargs, shift);
339  setConjugateMatrixN(u);
340  statevec_multiControlledMultiQubitUnitary(qureg, ctrlMask<<shift, targs, numTargs, u);
341  shiftIndices(targs, numTargs, -shift);
342  setConjugateMatrixN(u);
343  }
344 
345  qasm_recordComment(qureg, "Here, an undisclosed multi-controlled multi-qubit unitary was applied.");
346 }

References getQubitBitMask(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordComment(), setConjugateMatrixN(), shiftIndices(), statevec_multiControlledMultiQubitUnitary(), validateMultiControlsMultiTargets(), and validateMultiQubitUnitaryMatrix().

Referenced by TEST_CASE().

◆ multiControlledMultiRotatePauli()

void multiControlledMultiRotatePauli ( Qureg  qureg,
int *  controlQubits,
int  numControls,
int *  targetQubits,
enum pauliOpType *  targetPaulis,
int  numTargets,
qreal  angle 
)

Apply a multi-controlled multi-target multi-Pauli rotation, also known as a controlled Pauli gadget.

This is the unitary

\[ |1\rangle\langle 1|^{\otimes\, \text{numControls}} \; \otimes \, \exp \left( - i \, \frac{\theta}{2} \; \bigotimes_{j}^{\text{numTargets}} \hat{\sigma}_j\right) \;\;+\;\; \sum\limits_{k=0}^{2^{\,\text{numControls}} - 2} |k\rangle\langle k| \otimes \text{I} \]

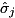where $\hat{\sigma}_j$ are the Pauli operators (pauliOpType) in targetPaulis, which operate upon the corresponding qubits in targetQubits.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-4, 1) {targets}; \node[draw=none] at (-4, 5) {controls}; \node[draw=none] at (0, 8) {$\vdots$}; \draw (0, 7) -- (0, 6); \draw (-2.5, 6) -- (2.5, 6); \draw[fill=black] (0, 6) circle (.2); \draw (0, 6) -- (0, 4); \draw (-2.5, 4) -- (2.5, 4); \draw[fill=black] (0, 4) circle (.2); \draw(0, 4) -- (0, 3); \draw (-2.5,0) -- (-1.5, 0); \draw (1.5, 0) -- (2.5, 0); \draw (-2.5,2) -- (-1.5, 2); \draw (1.5, 2) -- (2.5, 2); \draw (-1.5,-1)--(-1.5,3)--(1.5,3)--(1.5,-1); \node[draw=none] at (0, 1) {$e^{-i\frac{\theta}{2} \bigotimes\limits_j \hat{\sigma}_j }$}; \node[draw=none] at (0, -1) {$\vdots$}; \end{tikzpicture} \]

All qubits not appearing in targetQubits and controlQubits are assumed to receive the identity operator.

For example:

int numCtrls = 1;
int numTargs = 4;
int ctrls[] = {4};
int targs[] = {0,1,2,3};
pauliOpType paulis[] = {PAULI_X, PAULI_Y, PAULI_Z, PAULI_I};
multiControlledMultiRotatePauli(
qureg, ctrls, numCtrls, targs, paulis, numTargs, 0.1);

effects

\[ |1\rangle\langle 1 | \otimes \exp\left( -i \, (0.1/2) \, X_0 \, Y_1 \, Z_2 \right) \, \text{I}_3 \;\; + \;\; |0\rangle\langle 0| \otimes \text{I}^{\otimes 4} \]

on qureg, where unspecified qubits (along with those targeted by PAULI_I) are assumed to receive the identity operator (excluded from exponentiation).

This means specifying PAULI_I does not induce a global phase factor $\exp(-i \theta/2)$. Hence, if all targetPaulis are identity, then this function does nothing to qureg. Specifying PAULI_I on a qubit is superfluous but allowed for convenience.

This function effects the controlled Pauli gadget by first (controlled) rotating the qubits which are targeted with either X or Y into alternate basis, performing multiControlledMultiRotateZ() on all target qubits, then restoring the original basis.

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitslist of the indices of qubits to control upon
[in]numControlslength of length controlQubits
[in]targetQubitsa list of the indices of the target qubits
[in]targetPaulisa list of the Pauli operators around which to rotate the target qubits
[in]numTargetslength of list targetQubits
[in]anglethe angle by which the multi-qubit state is rotated around the Z axis
Exceptions
invalidQuESTInputError()
  • if any qubit in controlQubits and targetQubits is invalid, i.e. outside [0, qureg.numQubitsRepresented)
  • if controlQubits or targetQubits contain any repetitions
  • if any qubit in controlQubits is also in targetQubits (and vice versa)
  • if numTargets < 1
  • if numControls < 1 (use multiRotateZ() for no controls)
  • if any element of targetPaulis is not one of PAULI_I, PAULI_X, PAULI_Y, PAULI_Z
segmentation-fault
  • if controlQubits contains fewer elements than numControls
  • if targetQubits contains fewer elements than numTargets
  • if targetPaulis contains fewer elements than numTargets
Author
Tyson Jones

Definition at line 705 of file QuEST.c.

705  {
706  validateMultiControlsMultiTargets(qureg, controlQubits, numControls, targetQubits, numTargets, __func__);
707  validatePauliCodes(targetPaulis, numTargets, __func__);
708 
709  int conj=0;
710  long long int ctrlMask = getQubitBitMask(controlQubits, numControls);
711  statevec_multiControlledMultiRotatePauli(qureg, ctrlMask, targetQubits, targetPaulis, numTargets, angle, conj);
712  if (qureg.isDensityMatrix) {
713  conj = 1;
714  int shift = qureg.numQubitsRepresented;
715  shiftIndices(targetQubits, numTargets, shift);
716  statevec_multiControlledMultiRotatePauli(qureg, ctrlMask<<shift, targetQubits, targetPaulis, numTargets, angle, conj);
717  shiftIndices(targetQubits, numTargets, -shift);
718  }
719 
720  // @TODO: create actual QASM
721  qasm_recordComment(qureg,
722  "Here a %d-control %d-target multiControlledMultiRotatePauli of angle %g was performed (QASM not yet implemented)",
723  numControls, numTargets, angle);
724 }

References getQubitBitMask(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordComment(), shiftIndices(), statevec_multiControlledMultiRotatePauli(), validateMultiControlsMultiTargets(), and validatePauliCodes().

Referenced by TEST_CASE().

◆ multiControlledMultiRotateZ()

void multiControlledMultiRotateZ ( Qureg  qureg,
int *  controlQubits,
int  numControls,
int *  targetQubits,
int  numTargets,
qreal  angle 
)

Apply a multi-controlled multi-target Z rotation, also known as a controlled phase gadget.

This is the unitary

\[ |1\rangle\langle 1|^{\otimes\, \text{numControls}} \; \otimes \, \exp \left( - i \, \frac{\theta}{2} \; \bigotimes_{j}^{\text{numTargets}} Z_j\right) \;\;+\;\; \sum\limits_{k=0}^{2^{\,\text{numControls}} - 2} |k\rangle\langle k| \otimes \text{I} \]

where the Pauli Z gates operate upon the qubits in targetQubits, and cause rotations of 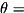$\theta =$ angle.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-4, 1) {targets}; \node[draw=none] at (-4, 5) {controls}; \node[draw=none] at (0, 8) {$\vdots$}; \draw (0, 7) -- (0, 6); \draw (-2.5, 6) -- (2.5, 6); \draw[fill=black] (0, 6) circle (.2); \draw (0, 6) -- (0, 4); \draw (-2.5, 4) -- (2.5, 4); \draw[fill=black] (0, 4) circle (.2); \draw(0, 4) -- (0, 3); \draw (-2.5,0) -- (-1.5, 0); \draw (1.5, 0) -- (2.5, 0); \draw (-2.5,2) -- (-1.5, 2); \draw (1.5, 2) -- (2.5, 2); \draw (-1.5,-1)--(-1.5,3)--(1.5,3)--(1.5,-1); \node[draw=none] at (0, 1) {$e^{-i\frac{\theta}{2}Z^{\otimes}}$}; \node[draw=none] at (0, -1) {$\vdots$}; \end{tikzpicture} \]

All qubits not appearing in targetQubits and controlQubits are assumed to receive the identity operator.

This has the effect of premultiplying all amplitudes (for which the control qubits are 1) with 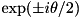$\exp(\pm i \theta/2)$, where the sign is determined by the parity of the target qubits for that amplitude.

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitslist of the indices of qubits to control upon
[in]numControlslength of length controlQubits
[in]targetQubitsa list of the indices of the target qubits
[in]numTargetslength of list targetQubits
[in]anglethe angle by which the multi-qubit state is rotated around the Z axis
Exceptions
invalidQuESTInputError()
  • if any qubit in controlQubits and targetQubits is invalid, i.e. outside [0, qureg.numQubitsRepresented)
  • if controlQubits or targetQubits contain any repetitions
  • if any qubit in controlQubits is also in targetQubits (and vice versa)
  • if numTargets < 1
  • if numControls < 1 (use multiRotateZ() for no controls)
segmentation-fault
  • if controlQubits contains fewer elements than numControls
  • if targetQubits contains fewer elements than numTargets
Author
Tyson Jones

Definition at line 668 of file QuEST.c.

668  {
669  validateMultiControlsMultiTargets(qureg, controlQubits, numControls, targetQubits, numTargets, __func__);
670 
671  long long int ctrlMask = getQubitBitMask(controlQubits, numControls);
672  long long int targMask = getQubitBitMask(targetQubits, numTargets);
673  statevec_multiControlledMultiRotateZ(qureg, ctrlMask, targMask, angle);
674  if (qureg.isDensityMatrix) {
675  int shift = qureg.numQubitsRepresented;
676  statevec_multiControlledMultiRotateZ(qureg, ctrlMask<<shift, targMask<<shift, - angle);
677  }
678 
679  // @TODO: create actual QASM
680  qasm_recordComment(qureg,
681  "Here a %d-control %d-target multiControlledMultiRotateZ of angle %g was performed (QASM not yet implemented)",
682  numControls, numTargets, angle);
683 }

References getQubitBitMask(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordComment(), statevec_multiControlledMultiRotateZ(), and validateMultiControlsMultiTargets().

Referenced by TEST_CASE().

◆ multiControlledPhaseFlip()

void multiControlledPhaseFlip ( Qureg  qureg,
int *  controlQubits,
int  numControlQubits 
)

Apply the multiple-qubit controlled phase flip gate, also known as the multiple-qubit controlled pauliZ gate.

For each state, if all control qubits have value one, multiply the amplitude of that state by -1. This applies the many-qubit unitary:

\[ \begin{pmatrix} 1 \\ & 1 \\\ & & \ddots \\ & & & 1 \\ & & & & -1 \end{pmatrix} \]

on the control qubits.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {controls}; \node[draw=none] at (0, 6) {$\vdots$}; \draw (0, 5) -- (0, 4); \draw (-2, 4) -- (2, 4); \draw[fill=black] (0, 4) circle (.2); \draw (0, 4) -- (0, 2); \draw (-2, 2) -- (2, 2); \draw[fill=black] (0, 2) circle (.2); \draw (0, 2) -- (0, 0); \draw (-2,0) -- (2, 0); \draw[fill=black] (0, 0) circle (.2); \end{tikzpicture} \]

Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitsarray of input qubits
[in]numControlQubitsnumber of input qubits
Exceptions
invalidQuESTInputError()
  • if numControlQubits is outside [1, qureg.numQubitsRepresented)
  • if any qubit in controlQubits is outside [0, qureg.numQubitsRepresented)
  • if any qubit in qubits is repeated
Author
Tyson Jones

Definition at line 587 of file QuEST.c.

587  {
588  validateMultiQubits(qureg, controlQubits, numControlQubits, __func__);
589 
590  statevec_multiControlledPhaseFlip(qureg, controlQubits, numControlQubits);
591  if (qureg.isDensityMatrix) {
592  int shift = qureg.numQubitsRepresented;
593  shiftIndices(controlQubits, numControlQubits, shift);
594  statevec_multiControlledPhaseFlip(qureg, controlQubits, numControlQubits);
595  shiftIndices(controlQubits, numControlQubits, -shift);
596  }
597 
598  qasm_recordMultiControlledGate(qureg, GATE_SIGMA_Z, controlQubits, numControlQubits-1, controlQubits[numControlQubits-1]);
599 }

References GATE_SIGMA_Z, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordMultiControlledGate(), shiftIndices(), statevec_multiControlledPhaseFlip(), and validateMultiQubits().

Referenced by TEST_CASE().

◆ multiControlledPhaseShift()

void multiControlledPhaseShift ( Qureg  qureg,
int *  controlQubits,
int  numControlQubits,
qreal  angle 
)

Introduce a phase factor 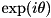$ \exp(i \theta) $ on state $ |1 \dots 1 \rangle $ of the passed qubits.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {controls}; \node[draw=none] at (1, .7) {$\theta$}; \node[draw=none] at (0, 6) {$\vdots$}; \draw (0, 5) -- (0, 4); \draw (-2, 4) -- (2, 4); \draw[fill=black] (0, 4) circle (.2); \draw (0, 4) -- (0, 2); \draw (-2, 2) -- (2, 2); \draw[fill=black] (0, 2) circle (.2); \draw (0, 2) -- (0, 0); \draw (-2,0) -- (2, 0); \draw[fill=black] (0, 0) circle (.2); \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitsarray of qubits to phase shift
[in]numControlQubitsthe length of array controlQubits
[in]angleamount by which to shift the phase in radians
Exceptions
invalidQuESTInputError()
  • if numControlQubits is outside [1, qureg.numQubitsRepresented])
  • if any qubit index in controlQubits is outside [0, qureg.numQubitsRepresented])
  • if the qubits in controlQubits are not unique
Author
Tyson Jones

Definition at line 510 of file QuEST.c.

510  {
511  validateMultiQubits(qureg, controlQubits, numControlQubits, __func__);
512 
513  statevec_multiControlledPhaseShift(qureg, controlQubits, numControlQubits, angle);
514  if (qureg.isDensityMatrix) {
515  int shift = qureg.numQubitsRepresented;
516  shiftIndices(controlQubits, numControlQubits, shift);
517  statevec_multiControlledPhaseShift(qureg, controlQubits, numControlQubits, -angle);
518  shiftIndices(controlQubits, numControlQubits, -shift);
519  }
520 
521  qasm_recordMultiControlledParamGate(qureg, GATE_PHASE_SHIFT, controlQubits, numControlQubits-1, controlQubits[numControlQubits-1], angle);
522 }

References GATE_PHASE_SHIFT, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordMultiControlledParamGate(), shiftIndices(), statevec_multiControlledPhaseShift(), and validateMultiQubits().

Referenced by TEST_CASE().

◆ multiControlledTwoQubitUnitary()

void multiControlledTwoQubitUnitary ( Qureg  qureg,
int *  controlQubits,
int  numControlQubits,
int  targetQubit1,
int  targetQubit2,
ComplexMatrix4  u 
)

Apply a general multi-controlled two-qubit unitary (including a global phase factor).

Any number of control qubits can be specified, and if all have value 1, the given unitary is applied to the target qubit. This effects the many-qubit unitary

\[ \begin{pmatrix} 1 \\ & 1 \\\ & & \ddots \\ & & & u_{00} & u_{01} & u_{02} & u_{03} \\ & & & u_{10} & u_{11} & u_{12} & u_{13} \\ & & & u_{20} & u_{21} & u_{22} & u_{23} \\ & & & u_{30} & u_{31} & u_{32} & u_{33} \end{pmatrix} \]

on the control and target qubits.

targetQubit1 is treated as the least significant qubit in u, such that a row in u is dotted with the vector 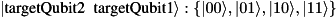$ |\text{targetQubit2} \;\; \text{targetQubit1}\rangle : \{ |00\rangle, |01\rangle, |10\rangle, |11\rangle \} $

The passed 4x4 ComplexMatrix must be unitary, otherwise an error is thrown.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {target1}; \node[draw=none] at (-3.5, 2) {target2}; \node[draw=none] at (-3.5, 5) {controls}; \node[draw=none] at (0, 8) {$\vdots$}; \draw (0, 7) -- (0, 6); \draw (-2, 6) -- (2, 6); \draw[fill=black] (0, 6) circle (.2); \draw (0, 6) -- (0, 4); \draw (-2, 4) -- (2, 4); \draw[fill=black] (0, 4) circle (.2); \draw(0, 4) -- (0, 3); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-2,2) -- (-1, 2); \draw (1, 2) -- (2, 2); \draw (-1,-1)--(-1,3)--(1,3)--(1,-1)--cycle; \node[draw=none] at (0, 1) {U}; \end{tikzpicture} \]

Note that in distributed mode, this routine requires that each node contains at least 4 amplitudes. This means an q-qubit register (state vector or density matrix) can be distributed by at most 2^q/4 nodes.

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitsthe control qubits which all must be in state 1 to effect the given unitary
[in]numControlQubitsthe number of control qubits
[in]targetQubit1first target qubit, treated as least significant in u
[in]targetQubit2second target qubit, treated as most significant in u
[in]uunitary matrix to apply
Exceptions
invalidQuESTInputError()
  • if targetQubit1 or targetQubit2 are outside [0, qureg.numQubitsRepresented)
  • if targetQubit1 equals targetQubit2
  • if any qubit in controlQubits is outside [0, qureg.numQubitsRepresented)
  • if controlQubits are not unique
  • if either targetQubit1 and targetQubit2 are in controlQubits
  • if matrix u is not unitary
  • if each node cannot fit 4 amplitudes in distributed mode
Author
Tyson Jones

Definition at line 282 of file QuEST.c.

282  {
283  validateMultiControlsMultiTargets(qureg, controlQubits, numControlQubits, (int[]) {targetQubit1, targetQubit2}, 2, __func__);
284  validateTwoQubitUnitaryMatrix(qureg, u, __func__);
285 
286  long long int ctrlQubitsMask = getQubitBitMask(controlQubits, numControlQubits);
287  statevec_multiControlledTwoQubitUnitary(qureg, ctrlQubitsMask, targetQubit1, targetQubit2, u);
288  if (qureg.isDensityMatrix) {
289  int shift = qureg.numQubitsRepresented;
290  statevec_multiControlledTwoQubitUnitary(qureg, ctrlQubitsMask<<shift, targetQubit1+shift, targetQubit2+shift, getConjugateMatrix4(u));
291  }
292 
293  qasm_recordComment(qureg, "Here, an undisclosed multi-controlled 2-qubit unitary was applied.");
294 }

References getConjugateMatrix4(), getQubitBitMask(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordComment(), statevec_multiControlledTwoQubitUnitary(), validateMultiControlsMultiTargets(), and validateTwoQubitUnitaryMatrix().

Referenced by TEST_CASE().

◆ multiControlledUnitary()

void multiControlledUnitary ( Qureg  qureg,
int *  controlQubits,
int  numControlQubits,
int  targetQubit,
ComplexMatrix2  u 
)

Apply a general multiple-control single-target unitary, which can include a global phase factor.

Any number of control qubits can be specified, and if all have value 1, the given unitary is applied to the target qubit. This effects the many-qubit unitary

\[ \begin{pmatrix} 1 \\ & 1 \\\ & & \ddots \\ & & & u_{00} & u_{01}\\ & & & u_{10} & u_{11} \end{pmatrix} \]

on the control and target qubits. The given 2x2 ComplexMatrix must be unitary, otherwise an error is thrown.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 3) {controls}; \node[draw=none] at (-3.5, 0) {target}; \node[draw=none] at (0, 6) {$\vdots$}; \draw (0, 5) -- (0, 4); \draw (-2, 4) -- (2, 4); \draw[fill=black] (0, 4) circle (.2); \draw (0, 4) -- (0, 2); \draw (-2, 2) -- (2, 2); \draw[fill=black] (0, 2) circle (.2); \draw (0, 2) -- (0, 1); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {U}; \end{tikzpicture} \]

See also


Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitsapplies unitary if all qubits in this array equal 1
[in]numControlQubitsnumber of control qubits
[in]targetQubitqubit to operate on
[in]usingle-qubit unitary matrix to apply
Exceptions
invalidQuESTInputError()
  • if numControlQubits is outside [1, qureg.numQubitsRepresented])
  • if any qubit index (targetQubit or one in controlQubits) is outside [0, qureg.numQubitsRepresented])
  • if any qubit in controlQubits is repeated
  • if controlQubits contains targetQubit
  • if u is not unitary
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 373 of file QuEST.c.

373  {
374  validateMultiControlsTarget(qureg, controlQubits, numControlQubits, targetQubit, __func__);
375  validateOneQubitUnitaryMatrix(u, __func__);
376 
377  long long int ctrlQubitsMask = getQubitBitMask(controlQubits, numControlQubits);
378  long long int ctrlFlipMask = 0;
379  statevec_multiControlledUnitary(qureg, ctrlQubitsMask, ctrlFlipMask, targetQubit, u);
380  if (qureg.isDensityMatrix) {
381  int shift = qureg.numQubitsRepresented;
382  statevec_multiControlledUnitary(qureg, ctrlQubitsMask<<shift, ctrlFlipMask<<shift, targetQubit+shift, getConjugateMatrix2(u));
383  }
384 
385  qasm_recordMultiControlledUnitary(qureg, u, controlQubits, numControlQubits, targetQubit);
386 }

References getConjugateMatrix2(), getQubitBitMask(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordMultiControlledUnitary(), statevec_multiControlledUnitary(), validateMultiControlsTarget(), and validateOneQubitUnitaryMatrix().

Referenced by TEST_CASE().

◆ multiQubitNot()

void multiQubitNot ( Qureg  qureg,
int *  targs,
int  numTargs 
)

Apply a NOT (or Pauli X) gate with multiple target qubits, which has the same effect as (but is much faster than) applying each single-qubit NOT gate in turn.

The ordering within targs has no effect on the operation.

This function is equivalent, but significantly faster (approximately numTargs times) than applying pauliX() on each qubit in targs in turn.

\[ X_a \otimes X_b \otimes \dots \]

The effected unitary, if targs happen to be contiguous, has matrix:

\[ \begin{pmatrix} & & & {{\scriptstyle\cdot}^{{\scriptstyle\cdot}^{{\scriptstyle\cdot}}}} \\ & & 1 & \\ & 1 & & \\ {{\scriptstyle\cdot}^{{\scriptstyle\cdot}^{{\scriptstyle\cdot}}}} & & & \end{pmatrix} \]

and circuit diagram:

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 1) {targets}; \draw (0, -1) -- (0, 2.4); \draw (-2,2) -- (2, 2); \draw (0, 2) circle (.4); \draw (-2,0) -- (2, 0); \draw (0, 0) circle (.4); \node[draw=none] at (0, -1.5) {$\vdots$}; \end{tikzpicture} \]

In distributed mode, this operation requires at most a single round of pair-wise communication between nodes, and hence is as efficient as pauliX().

See also
Parameters
[in,out]qurega state-vector or density matrix to modify
[in]targsa list of the qubits to be targeted by the X gates
[in]numTargsthe length of list targs
Exceptions
invalidQuESTInputError()
  • if any qubit in targs is invalid, i.e. outside [0, qureg.numQubitsRepresented)
  • if targs contain any repetitions
  • if numTargs < 1
  • if numTargs >qureg.numQubitsRepresented
segmentation-fault
  • if targs contains fewer elements than numTargs
Author
Tyson Jones

Definition at line 536 of file QuEST.c.

536  {
537  validateMultiTargets(qureg, targs, numTargs, __func__);
538 
539  long long int targMask = getQubitBitMask(targs, numTargs);
540  statevec_multiControlledMultiQubitNot(qureg, 0, targMask);
541  if (qureg.isDensityMatrix) {
542  int shift = qureg.numQubitsRepresented;
543  statevec_multiControlledMultiQubitNot(qureg, 0, targMask<<shift);
544  }
545 
546  qasm_recordMultiControlledMultiQubitNot(qureg, NULL, 0, targs, numTargs);
547 }

References getQubitBitMask(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordMultiControlledMultiQubitNot(), statevec_multiControlledMultiQubitNot(), and validateMultiTargets().

Referenced by TEST_CASE().

◆ multiQubitUnitary()

void multiQubitUnitary ( Qureg  qureg,
int *  targs,
int  numTargs,
ComplexMatrixN  u 
)

Apply a general multi-qubit unitary (including a global phase factor) with any number of target qubits.

The first target qubit in targs is treated as least significant in u. For example,

multiQubitUnitary(qureg, (int []) {a, b, c}, 3, u);

will invoke multiplication

\[ \begin{pmatrix} u_{00} & u_{01} & u_{02} & u_{03} & u_{04} & u_{05} & u_{06} & u_{07} \\ u_{10} & u_{11} & u_{12} & u_{13} & u_{14} & u_{15} & u_{16} & u_{17} \\ u_{20} & u_{21} & u_{22} & u_{23} & u_{24} & u_{25} & u_{26} & u_{27} \\ u_{30} & u_{31} & u_{32} & u_{33} & u_{34} & u_{35} & u_{36} & u_{37} \\ u_{40} & u_{41} & u_{42} & u_{43} & u_{44} & u_{45} & u_{46} & u_{47} \\ u_{50} & u_{51} & u_{52} & u_{53} & u_{54} & u_{55} & u_{56} & u_{57} \\ u_{60} & u_{61} & u_{62} & u_{63} & u_{64} & u_{65} & u_{66} & u_{67} \\ u_{70} & u_{71} & u_{72} & u_{73} & u_{74} & u_{75} & u_{76} & u_{77} \\ \end{pmatrix} \begin{pmatrix} |cba\rangle = |000\rangle \\ |cba\rangle = |001\rangle \\ |cba\rangle = |010\rangle \\ |cba\rangle = |011\rangle \\ |cba\rangle = |100\rangle \\ |cba\rangle = |101\rangle \\ |cba\rangle = |110\rangle \\ |cba\rangle = |111\rangle \end{pmatrix} \]

The passed ComplexMatrix must be unitary and be a compatible size with the specified number of target qubits, otherwise an error is thrown.

To left-multiply a non-unitary ComplexMatrixN, use applyMatrixN().

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 1) {targets}; \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-2,2) -- (-1, 2); \draw (1, 2) -- (2, 2); \draw (-1,-1)--(-1,3)--(1,3)--(1,-1); \node[draw=none] at (0, 1) {U}; \node[draw=none] at (0, -1) {$\vdots$}; \end{tikzpicture} \]

Note that in multithreaded mode, each thread will clone 2^numTargs amplitudes, and store these in the runtime stack. Using t threads, the total memory overhead of this function is t*2^numTargs. For many targets (e.g. 16 qubits), this may cause a stack-overflow / seg-fault (e.g. on a 1 MiB stack).

Note too that in distributed mode, this routine requires that each node contains at least 2^numTargs amplitudes in the register. This means an q-qubit register (state vector or density matrix) can be distributed by at most 2^q / 2^numTargs nodes.

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]targsa list of the target qubits, ordered least significant to most in u
[in]numTargsthe number of target qubits
[in]uunitary matrix to apply
Exceptions
invalidQuESTInputError()
  • if any index in targs is outside of [0, qureg.numQubitsRepresented)
  • if targs are not unique
  • if matrix u is not unitary
  • if u is not of a compatible size with numTargs
  • if a node cannot fit the required number of target amplitudes in distributed mode
Author
Tyson Jones

Definition at line 296 of file QuEST.c.

296  {
297  validateMultiTargets(qureg, targs, numTargs, __func__);
298  validateMultiQubitUnitaryMatrix(qureg, u, numTargs, __func__);
299 
300  statevec_multiQubitUnitary(qureg, targs, numTargs, u);
301  if (qureg.isDensityMatrix) {
302  int shift = qureg.numQubitsRepresented;
303  shiftIndices(targs, numTargs, shift);
304  setConjugateMatrixN(u);
305  statevec_multiQubitUnitary(qureg, targs, numTargs, u);
306  shiftIndices(targs, numTargs, -shift);
307  setConjugateMatrixN(u);
308  }
309 
310  qasm_recordComment(qureg, "Here, an undisclosed multi-qubit unitary was applied.");
311 }

References Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordComment(), setConjugateMatrixN(), shiftIndices(), statevec_multiQubitUnitary(), validateMultiQubitUnitaryMatrix(), and validateMultiTargets().

Referenced by TEST_CASE().

◆ multiRotatePauli()

void multiRotatePauli ( Qureg  qureg,
int *  targetQubits,
enum pauliOpType *  targetPaulis,
int  numTargets,
qreal  angle 
)

Apply a multi-qubit multi-Pauli rotation, also known as a Pauli gadget, on a selected number of qubits.

This is the unitary

\[ \exp \left( - i \, \frac{\theta}{2} \; \bigotimes_{j}^{\text{numTargets}} \hat{\sigma}_j\right) \]

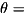
where $\theta = $angle and 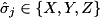$\hat{\sigma}_j \in \{X, Y, Z\}$ is a Pauli operator pauliOpType operating upon the corresponding qubit targetQubits.

For example:

multiRotatePauli(qureg, (int[]) {4,5,8,9}, (int[]) {0,1,2,3}, 4, .1)

effects

\[ \exp \left( - i \, (0.1/2) \; X_5 \, Y_8 \, Z_9 \right) \]

on qureg, where unspecified qubits (along with those targeted by PAULI_I) are assumed to receive the identity operator (excluded from exponentiation).

This means specifying PAULI_I does not induce a global phase factor $\exp(-i \theta/2)$. Hence, if all targetPaulis are identity, then this function does nothing to qureg. Specifying PAULI_I on a qubit is superfluous but allowed for convenience.

This function effects the Pauli gadget by first rotating the qubits which are nominated to receive X or Y Paulis into alternate basis, performing multiRotateZ() on all target qubits, then restoring the original basis.

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]targetQubitsa list of the indices of the target qubits
[in]targetPaulisa list of the Pauli operators (pauliOpType) to apply to the corresponding qubits in targetQubits
[in]numTargetsnumber of target qubits, i.e. the length of targetQubits and targetPaulis
[in]anglethe angle by which the multi-qubit state is rotated
Exceptions
invalidQuESTInputError()
  • if numTargets is outside [1, qureg.numQubitsRepresented)
  • if any qubit in targetQubits is outside [0, qureg.numQubitsRepresented)
  • if any qubit in targetQubits is repeated
  • if any element of targetPaulis is not one of PAULI_I, PAULI_X, PAULI_Y, PAULI_Z
segmentation-fault
  • if targetQubits contains fewer elements than numTargets
  • if targetPaulis contains fewer elements than numTargets
Author
Tyson Jones

Definition at line 685 of file QuEST.c.

685  {
686  validateMultiTargets(qureg, targetQubits, numTargets, __func__);
687  validatePauliCodes(targetPaulis, numTargets, __func__);
688 
689  int conj=0;
690  statevec_multiRotatePauli(qureg, targetQubits, targetPaulis, numTargets, angle, conj);
691  if (qureg.isDensityMatrix) {
692  conj = 1;
693  int shift = qureg.numQubitsRepresented;
694  shiftIndices(targetQubits, numTargets, shift);
695  statevec_multiRotatePauli(qureg, targetQubits, targetPaulis, numTargets, angle, conj);
696  shiftIndices(targetQubits, numTargets, -shift);
697  }
698 
699  // @TODO: create actual QASM
700  qasm_recordComment(qureg,
701  "Here a %d-qubit multiRotatePauli of angle %g was performed (QASM not yet implemented)",
702  numTargets, angle);
703 }

References Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordComment(), shiftIndices(), statevec_multiRotatePauli(), validateMultiTargets(), and validatePauliCodes().

Referenced by TEST_CASE().

◆ multiRotateZ()

void multiRotateZ ( Qureg  qureg,
int *  qubits,
int  numQubits,
qreal  angle 
)

Apply a multi-qubit Z rotation, also known as a phase gadget, on a selected number of qubits.

This is the unitary

\[ \exp \left( - i \, \frac{\theta}{2} \; \bigotimes_{j}^{\text{numQubits}} Z_j\right) \]

where the Pauli Z gates operate the qubits listed in qubits, and cause rotations of 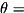$\theta =$ angle.

All qubits not appearing in qubits are assumed to receive the identity operator.

This has the effect of premultiplying every amplitude with 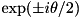$\exp(\pm i \theta/2)$ where the sign is determined by the parity of the target qubits for that amplitude.

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]qubitsa list of the indices of the target qubits
[in]numQubitsnumber of target qubits
[in]anglethe angle by which the multi-qubit state is rotated around the Z axis
Exceptions
invalidQuESTInputError()
  • if numQubits is outside [1, qureg.numQubitsRepresented])
  • if any qubit in qubits is outside [0, qureg.numQubitsRepresented])
  • if any qubit in qubits is repeated
segmentation-fault
  • if qubits contains fewer elements than numQubits
Author
Tyson Jones

Definition at line 652 of file QuEST.c.

652  {
653  validateMultiTargets(qureg, qubits, numQubits, __func__);
654 
655  long long int mask = getQubitBitMask(qubits, numQubits);
656  statevec_multiRotateZ(qureg, mask, angle);
657  if (qureg.isDensityMatrix) {
658  int shift = qureg.numQubitsRepresented;
659  statevec_multiRotateZ(qureg, mask << shift, -angle);
660  }
661 
662  // @TODO: create actual QASM
663  qasm_recordComment(qureg,
664  "Here a %d-qubit multiRotateZ of angle %g was performed (QASM not yet implemented)",
665  numQubits, angle);
666 }

References getQubitBitMask(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordComment(), statevec_multiRotateZ(), and validateMultiTargets().

Referenced by TEST_CASE().

◆ multiStateControlledUnitary()

void multiStateControlledUnitary ( Qureg  qureg,
int *  controlQubits,
int *  controlState,
int  numControlQubits,
int  targetQubit,
ComplexMatrix2  u 
)

Apply a general single-qubit unitary with multiple control qubits, conditioned upon a specific bit sequence.

Any number of control qubits can be specified, along with their classical state (0 or 1) to condition upon. Only amplitudes of computational basis states for which controlQubits have corresponding bit values controlState are modified by u.

This function is equivalent (albeit faster) to applying pauliX() on each of the control qubits which are conditioned on outcome 0, calling multiControlledUnitary(), then re-appplying pauliX() on the same qubits.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 3) {controls}; \node[draw=none] at (-3.5, 0) {target}; \node[draw=none] at (0, 6) {$\vdots$}; \draw (0, 5) -- (0, 4); \draw (-2, 4) -- (2, 4); \draw[fill=black] (0, 4) circle (.2); \draw (0, 4) -- (0, 2); \draw (-2, 2) -- (2, 2); \draw[fill=white] (0, 2) circle (.2); \draw (0, 2-.2) -- (0, 1); \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {U}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]controlQubitsthe indices of the control qubits
[in]controlStatethe bit values (0 or 1) of each control qubit, upon which to condition
[in]numControlQubitsnumber of control qubits
[in]targetQubitqubit to operate the unitary upon
[in]usingle-qubit unitary matrix to apply
Exceptions
invalidQuESTInputError()
  • if numControlQubits is outside [1, qureg.numQubitsRepresented])
  • if any qubit index (targetQubit or one in controlQubits) is outside [0, qureg.numQubitsRepresented]),
  • if any qubit in controlQubits is repeated
  • if controlQubits contains targetQubit
  • if any element of controlState is not a bit (0 or 1)
  • if u is not unitary
Author
Tyson Jones

Definition at line 388 of file QuEST.c.

388  {
389  validateMultiControlsTarget(qureg, controlQubits, numControlQubits, targetQubit, __func__);
390  validateOneQubitUnitaryMatrix(u, __func__);
391  validateControlState(controlState, numControlQubits, __func__);
392 
393  long long int ctrlQubitsMask = getQubitBitMask(controlQubits, numControlQubits);
394  long long int ctrlFlipMask = getControlFlipMask(controlQubits, controlState, numControlQubits);
395  statevec_multiControlledUnitary(qureg, ctrlQubitsMask, ctrlFlipMask, targetQubit, u);
396  if (qureg.isDensityMatrix) {
397  int shift = qureg.numQubitsRepresented;
398  statevec_multiControlledUnitary(qureg, ctrlQubitsMask<<shift, ctrlFlipMask<<shift, targetQubit+shift, getConjugateMatrix2(u));
399  }
400 
401  qasm_recordMultiStateControlledUnitary(qureg, u, controlQubits, controlState, numControlQubits, targetQubit);
402 }

References getConjugateMatrix2(), getControlFlipMask(), getQubitBitMask(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordMultiStateControlledUnitary(), statevec_multiControlledUnitary(), validateControlState(), validateMultiControlsTarget(), and validateOneQubitUnitaryMatrix().

Referenced by TEST_CASE().

◆ pauliX()

void pauliX ( Qureg  qureg,
int  targetQubit 
)

Apply the single-qubit Pauli-X (also known as the X, sigma-X, NOT or bit-flip) gate.

This is a rotation of 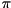$\pi$ around the x-axis on the Bloch sphere. I.e.

\[ \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \]

with circuit diagram:

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {target}; \draw (-2,0) -- (2, 0); \draw (0, 0) circle (.5); \draw (0, .5) -- (0, -.5); \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]targetQubitqubit to operate on
Exceptions
invalidQuESTInputError()
  • if targetQubit is outside [0, qureg.numQubitsRepresented)
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 432 of file QuEST.c.

432  {
433  validateTarget(qureg, targetQubit, __func__);
434 
435  statevec_pauliX(qureg, targetQubit);
436  if (qureg.isDensityMatrix) {
437  statevec_pauliX(qureg, targetQubit+qureg.numQubitsRepresented);
438  }
439 
440  qasm_recordGate(qureg, GATE_SIGMA_X, targetQubit);
441 }

References GATE_SIGMA_X, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordGate(), statevec_pauliX(), and validateTarget().

Referenced by TEST_CASE().

◆ pauliY()

void pauliY ( Qureg  qureg,
int  targetQubit 
)

Apply the single-qubit Pauli-Y (also known as the Y or sigma-Y) gate.

This is a rotation of 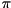$\pi$ around the Y-axis on the Bloch sphere. I.e.

\[ \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} \]

with circuit diagram:

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {target}; \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {$\sigma_y$}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]targetQubitqubit to operate on
Exceptions
invalidQuESTInputError()
  • if targetQubit is outside [0, qureg.numQubitsRepresented)
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 443 of file QuEST.c.

443  {
444  validateTarget(qureg, targetQubit, __func__);
445 
446  statevec_pauliY(qureg, targetQubit);
447  if (qureg.isDensityMatrix) {
448  statevec_pauliYConj(qureg, targetQubit + qureg.numQubitsRepresented);
449  }
450 
451  qasm_recordGate(qureg, GATE_SIGMA_Y, targetQubit);
452 }

References GATE_SIGMA_Y, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordGate(), statevec_pauliY(), statevec_pauliYConj(), and validateTarget().

Referenced by TEST_CASE().

◆ pauliZ()

void pauliZ ( Qureg  qureg,
int  targetQubit 
)

Apply the single-qubit Pauli-Z (also known as the Z, sigma-Z or phase-flip) gate.

This is a rotation of 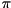$\pi$ around the Z-axis (a phase shift) on the Bloch sphere. I.e.

\[ \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \]

with circuit diagram:

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {target}; \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {$\sigma_z$}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]targetQubitqubit to operate on
Exceptions
invalidQuESTInputError()
  • if targetQubit is outside [0, qureg.numQubitsRepresented)
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 454 of file QuEST.c.

454  {
455  validateTarget(qureg, targetQubit, __func__);
456 
457  statevec_pauliZ(qureg, targetQubit);
458  if (qureg.isDensityMatrix) {
459  statevec_pauliZ(qureg, targetQubit+qureg.numQubitsRepresented);
460  }
461 
462  qasm_recordGate(qureg, GATE_SIGMA_Z, targetQubit);
463 }

References GATE_SIGMA_Z, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordGate(), statevec_pauliZ(), and validateTarget().

Referenced by TEST_CASE().

◆ phaseShift()

void phaseShift ( Qureg  qureg,
int  targetQubit,
qreal  angle 
)

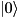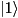Shift the phase between $ |0\rangle $ and $ |1\rangle $ of a single qubit by a given angle.

This is equivalent to a Z-axis rotation of the Bloch-sphere up to a global phase factor.

For angle 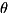$\theta$, this effects single-qubit unitary

\[ \begin{pmatrix} 1 & 0 \\ 0 & \exp(i \theta) \end{pmatrix} \]

with circuit diagram

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-4, 0) {targetQubit}; \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {$R_\theta$}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]targetQubitqubit to undergo a phase shift
[in]angleamount by which to shift the phase in radians
Exceptions
invalidQuESTInputError()
  • targetQubit is outside [0, qureg.numQubitsRepresented).
Author
Tyson Jones

Definition at line 487 of file QuEST.c.

487  {
488  validateTarget(qureg, targetQubit, __func__);
489 
490  statevec_phaseShift(qureg, targetQubit, angle);
491  if (qureg.isDensityMatrix) {
492  statevec_phaseShift(qureg, targetQubit+qureg.numQubitsRepresented, -angle);
493  }
494 
495  qasm_recordParamGate(qureg, GATE_PHASE_SHIFT, targetQubit, angle);
496 }

References GATE_PHASE_SHIFT, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordParamGate(), statevec_phaseShift(), and validateTarget().

Referenced by TEST_CASE().

◆ rotateAroundAxis()

void rotateAroundAxis ( Qureg  qureg,
int  rotQubit,
qreal  angle,
Vector  axis 
)

Rotate a single qubit by a given angle around a given Vector on the Bloch-sphere.


The vector must not be zero (else an error is thrown), but needn't be unit magnitude, since it will be normalised by QuEST.

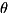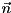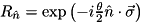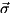For angle $\theta$ and axis vector $\vec{n}$, applies $R_{\hat{n}} = \exp \left(- i \frac{\theta}{2} \hat{n} \cdot \vec{\sigma} \right) $ where $\vec{\sigma}$ is the vector of Pauli matrices.

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]rotQubitqubit to rotate
[in]angleangle by which to rotate in radians
[in]axisvector around which to rotate (can be non-unit; will be normalised)
Exceptions
invalidQuESTInputError()
  • if rotQubit is outside [0, qureg.numQubitsRepresented)
  • if axis is the zero vector
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 601 of file QuEST.c.

601  {
602  validateTarget(qureg, rotQubit, __func__);
603  validateVector(axis, __func__);
604 
605  statevec_rotateAroundAxis(qureg, rotQubit, angle, axis);
606  if (qureg.isDensityMatrix) {
607  int shift = qureg.numQubitsRepresented;
608  statevec_rotateAroundAxisConj(qureg, rotQubit+shift, angle, axis);
609  }
610 
611  qasm_recordAxisRotation(qureg, angle, axis, rotQubit);
612 }

References Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordAxisRotation(), statevec_rotateAroundAxis(), statevec_rotateAroundAxisConj(), validateTarget(), and validateVector().

Referenced by TEST_CASE().

◆ rotateX()

void rotateX ( Qureg  qureg,
int  rotQubit,
qreal  angle 
)

Rotate a single qubit by a given angle around the X-axis of the Bloch-sphere.

For angle 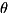$\theta$, applies

\[ \begin{pmatrix} \cos\theta/2 & -i \sin \theta/2\\ -i \sin \theta/2 & \cos \theta/2 \end{pmatrix} \]

with circuit diagram:

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {rot}; \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {$R_x(\theta)$}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]rotQubitqubit to rotate
[in]angleangle by which to rotate in radians
Exceptions
invalidQuESTInputError()
  • if rotQubit is outside [0, qureg.numQubitsRepresented)
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 187 of file QuEST.c.

187  {
188  validateTarget(qureg, targetQubit, __func__);
189 
190  statevec_rotateX(qureg, targetQubit, angle);
191  if (qureg.isDensityMatrix) {
192  statevec_rotateX(qureg, targetQubit+qureg.numQubitsRepresented, -angle);
193  }
194 
195  qasm_recordParamGate(qureg, GATE_ROTATE_X, targetQubit, angle);
196 }

References GATE_ROTATE_X, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordParamGate(), statevec_rotateX(), and validateTarget().

Referenced by TEST_CASE().

◆ rotateY()

void rotateY ( Qureg  qureg,
int  rotQubit,
qreal  angle 
)

Rotate a single qubit by a given angle around the Y-axis of the Bloch-sphere.

For angle 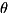$\theta$, applies

\[ \begin{pmatrix} \cos\theta/2 & - \sin \theta/2\\ \sin \theta/2 & \cos \theta/2 \end{pmatrix} \]

with circuit diagram:

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {rot}; \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {$R_y(\theta)$}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]rotQubitqubit to rotate
[in]angleangle by which to rotate in radians
Exceptions
invalidQuESTInputErrorif rotQubit is outside [0, qureg.numQubitsRepresented).
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc, debug)

Definition at line 198 of file QuEST.c.

198  {
199  validateTarget(qureg, targetQubit, __func__);
200 
201  statevec_rotateY(qureg, targetQubit, angle);
202  if (qureg.isDensityMatrix) {
203  statevec_rotateY(qureg, targetQubit+qureg.numQubitsRepresented, angle);
204  }
205 
206  qasm_recordParamGate(qureg, GATE_ROTATE_Y, targetQubit, angle);
207 }

References GATE_ROTATE_Y, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordParamGate(), statevec_rotateY(), and validateTarget().

Referenced by TEST_CASE().

◆ rotateZ()

void rotateZ ( Qureg  qureg,
int  rotQubit,
qreal  angle 
)

Rotate a single qubit by a given angle around the Z-axis of the Bloch-sphere (also known as a phase shift gate).


For angle 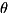$\theta$, applies

\[ \begin{pmatrix} \exp(-i \theta/2) & 0 \\ 0 & \exp(i \theta/2) \end{pmatrix} \]

with circuit diagram:

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {rot}; \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {$R_z(\theta)$}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]rotQubitqubit to rotate
[in]angleangle by which to rotate in radians
Exceptions
invalidQuESTInputError()
  • if rotQubit is outside [0, qureg.numQubitsRepresented)
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 209 of file QuEST.c.

209  {
210  validateTarget(qureg, targetQubit, __func__);
211 
212  statevec_rotateZ(qureg, targetQubit, angle);
213  if (qureg.isDensityMatrix) {
214  statevec_rotateZ(qureg, targetQubit+qureg.numQubitsRepresented, -angle);
215  }
216 
217  qasm_recordParamGate(qureg, GATE_ROTATE_Z, targetQubit, angle);
218 }

References GATE_ROTATE_Z, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordParamGate(), statevec_rotateZ(), and validateTarget().

Referenced by TEST_CASE().

◆ sGate()

void sGate ( Qureg  qureg,
int  targetQubit 
)

Apply the single-qubit S gate.

This is a rotation of 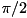$\pi/2$ around the Z-axis on the Bloch sphere, or the unitary:

\[ \begin{pmatrix} 1 & 0 \\ 0 & i \end{pmatrix} \]

with circuit diagram:

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {target}; \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {S}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]targetQubitqubit to operate upon
Exceptions
invalidQuESTInputError()
  • if targetQubit is outside [0, qureg.numQubitsRepresented)
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 465 of file QuEST.c.

465  {
466  validateTarget(qureg, targetQubit, __func__);
467 
468  statevec_sGate(qureg, targetQubit);
469  if (qureg.isDensityMatrix) {
470  statevec_sGateConj(qureg, targetQubit+qureg.numQubitsRepresented);
471  }
472 
473  qasm_recordGate(qureg, GATE_S, targetQubit);
474 }

References GATE_S, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordGate(), statevec_sGate(), statevec_sGateConj(), and validateTarget().

Referenced by TEST_CASE().

◆ sqrtSwapGate()

void sqrtSwapGate ( Qureg  qureg,
int  qb1,
int  qb2 
)

Performs a sqrt SWAP gate between qubit1 and qubit2.

This effects

\[ \begin{pmatrix} 1 \\ & \frac{1}{2}(1+i) & \frac{1}{2}(1-i) \\\ & \frac{1}{2}(1-i) & \frac{1}{2}(1+i) \\ & & & 1 \end{pmatrix} \]

on the designated qubits, though is performed internally by three CNOT gates.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {qubit1}; \node[draw=none] at (-3.5, 0) {qubit2}; \draw (-2, 2) -- (2, 2); \draw (0, 2) -- (0, 0); \draw (-2,0) -- (2, 0); \draw (-.35,-.35) -- (.35,.35); \draw (-.35,.35) -- (.35,-.35); \draw (-.35,-.35 + 2) -- (.35,.35 + 2); \draw (-.35,.35 + 2) -- (.35,-.35 + 2); \draw[fill=white] (0, 1) circle (.5); \node[draw=none] at (0, 1) {1/2}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]qb1qubit to sqrt swap
[in]qb2other qubit to sqrt swap
Exceptions
invalidQuESTInputError()
  • if either qubit1 or qubit2 are outside [0, qureg.numQubitsRepresented)
  • if qubit1 and qubit2 are equal
Author
Tyson Jones

Definition at line 639 of file QuEST.c.

639  {
640  validateUniqueTargets(qureg, qb1, qb2, __func__);
641  validateMultiQubitMatrixFitsInNode(qureg, 2, __func__); // uses 2qb unitary in QuEST_common
642 
643  statevec_sqrtSwapGate(qureg, qb1, qb2);
644  if (qureg.isDensityMatrix) {
645  int shift = qureg.numQubitsRepresented;
646  statevec_sqrtSwapGateConj(qureg, qb1+shift, qb2+shift);
647  }
648 
649  qasm_recordControlledGate(qureg, GATE_SQRT_SWAP, qb1, qb2);
650 }

References GATE_SQRT_SWAP, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordControlledGate(), statevec_sqrtSwapGate(), statevec_sqrtSwapGateConj(), validateMultiQubitMatrixFitsInNode(), and validateUniqueTargets().

Referenced by TEST_CASE().

◆ swapGate()

void swapGate ( Qureg  qureg,
int  qubit1,
int  qubit2 
)

Performs a SWAP gate between qubit1 and qubit2.

This effects

\[ \begin{pmatrix} 1 \\ & & 1 \\\ & 1 \\ & & & 1 \end{pmatrix} \]

on the designated qubits, though is performed internally by three CNOT gates.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 2) {qubit1}; \node[draw=none] at (-3.5, 0) {qubit2}; \draw (-2, 2) -- (2, 2); \draw (0, 2) -- (0, 0); \draw (-2,0) -- (2, 0); \draw (-.35,-.35) -- (.35,.35); \draw (-.35,.35) -- (.35,-.35); \draw (-.35,-.35 + 2) -- (.35,.35 + 2); \draw (-.35,.35 + 2) -- (.35,-.35 + 2); \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]qubit1qubit to swap
[in]qubit2other qubit to swap
Exceptions
invalidQuESTInputError()
  • if either qubit1 or qubit2 are outside [0, qureg.numQubitsRepresented)
  • if qubit1 and qubit2 are equal
Author
Tyson Jones

Definition at line 627 of file QuEST.c.

627  {
628  validateUniqueTargets(qureg, qb1, qb2, __func__);
629 
630  statevec_swapQubitAmps(qureg, qb1, qb2);
631  if (qureg.isDensityMatrix) {
632  int shift = qureg.numQubitsRepresented;
633  statevec_swapQubitAmps(qureg, qb1+shift, qb2+shift);
634  }
635 
636  qasm_recordControlledGate(qureg, GATE_SWAP, qb1, qb2);
637 }

References GATE_SWAP, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordControlledGate(), statevec_swapQubitAmps(), and validateUniqueTargets().

Referenced by TEST_CASE().

◆ tGate()

void tGate ( Qureg  qureg,
int  targetQubit 
)

Apply the single-qubit T gate.

This is a rotation of 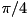$\pi/4$ around the Z-axis on the Bloch sphere, or the unitary:

\[ \begin{pmatrix} 1 & 0 \\ 0 & \exp\left(i \frac{\pi}{4}\right) \end{pmatrix} \]

with circuit diagram:

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {target}; \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {T}; \end{tikzpicture} \]

See also
Parameters
[in,out]quregobject representing the set of all qubits
[in]targetQubitqubit to operate upon
Exceptions
invalidQuESTInputError()
  • if targetQubit is outside [0, qureg.numQubitsRepresented)
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 476 of file QuEST.c.

476  {
477  validateTarget(qureg, targetQubit, __func__);
478 
479  statevec_tGate(qureg, targetQubit);
480  if (qureg.isDensityMatrix) {
481  statevec_tGateConj(qureg, targetQubit+qureg.numQubitsRepresented);
482  }
483 
484  qasm_recordGate(qureg, GATE_T, targetQubit);
485 }

References GATE_T, Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordGate(), statevec_tGate(), statevec_tGateConj(), and validateTarget().

Referenced by TEST_CASE().

◆ twoQubitUnitary()

void twoQubitUnitary ( Qureg  qureg,
int  targetQubit1,
int  targetQubit2,
ComplexMatrix4  u 
)

Apply a general two-qubit unitary (including a global phase factor).

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {target2}; \node[draw=none] at (-3.5, 2) {target1}; \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-2,2) -- (-1, 2); \draw (1, 2) -- (2, 2); \draw (-1,-1)--(-1,3)--(1,3)--(1,-1)--cycle; \node[draw=none] at (0, 1) {U}; \end{tikzpicture} \]

targetQubit1 is treated as the least significant qubit in u, such that a row in u is dotted with the vector 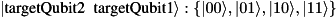$ |\text{targetQubit2} \;\; \text{targetQubit1}\rangle : \{ |00\rangle, |01\rangle, |10\rangle, |11\rangle \} $

For example,

twoQubitUnitary(qureg, a, b, u);

will invoke multiplication

\[ \begin{pmatrix} u_{00} & u_{01} & u_{02} & u_{03} \\ u_{10} & u_{11} & u_{12} & u_{13} \\ u_{20} & u_{21} & u_{22} & u_{23} \\ u_{30} & u_{31} & u_{32} & u_{33} \end{pmatrix} \begin{pmatrix} |ba\rangle = |00\rangle \\ |ba\rangle = |01\rangle \\ |ba\rangle = |10\rangle \\ |ba\rangle = |11\rangle \end{pmatrix} \]

The passed ComplexMatrix4 must be unitary, otherwise an error is thrown.

Use applyMatrix4() to left-multiply a non-unitary ComplexMatrix4.

Note that in distributed mode, this routine requires that each node contains at least 4 amplitudes. This means an q-qubit register (state vector or density matrix) can be distributed by at most 2^q/4 nodes.

See also


Parameters
[in,out]quregobject representing the set of all qubits
[in]targetQubit1first qubit to operate on, treated as least significant in u
[in]targetQubit2second qubit to operate on, treated as most significant in u
[in]uunitary matrix to apply
Exceptions
invalidQuESTInputError()
  • if targetQubit1 or targetQubit2 are outside [0, qureg.numQubitsRepresented)
  • if targetQubit1 equals targetQubit2
  • if matrix u is not unitary
  • if each node cannot fit 4 amplitudes in distributed mode
Author
Tyson Jones

Definition at line 256 of file QuEST.c.

256  {
257  validateMultiTargets(qureg, (int []) {targetQubit1, targetQubit2}, 2, __func__);
258  validateTwoQubitUnitaryMatrix(qureg, u, __func__);
259 
260  statevec_twoQubitUnitary(qureg, targetQubit1, targetQubit2, u);
261  if (qureg.isDensityMatrix) {
262  int shift = qureg.numQubitsRepresented;
263  statevec_twoQubitUnitary(qureg, targetQubit1+shift, targetQubit2+shift, getConjugateMatrix4(u));
264  }
265 
266  qasm_recordComment(qureg, "Here, an undisclosed 2-qubit unitary was applied.");
267 }

References getConjugateMatrix4(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordComment(), statevec_twoQubitUnitary(), validateMultiTargets(), and validateTwoQubitUnitaryMatrix().

Referenced by TEST_CASE().

◆ unitary()

void unitary ( Qureg  qureg,
int  targetQubit,
ComplexMatrix2  u 
)

Apply a general single-qubit unitary (including a global phase factor).

The passed 2x2 ComplexMatrix must be unitary, otherwise an error is thrown.

\[ \begin{tikzpicture}[scale=.5] \node[draw=none] at (-3.5, 0) {target}; \draw (-2,0) -- (-1, 0); \draw (1, 0) -- (2, 0); \draw (-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; \node[draw=none] at (0, 0) {U}; \end{tikzpicture} \]

If qureg is a state-vector, then the resulting state is 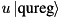$ u \, |\text{qureg}\rangle $.
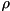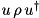If qureg is a density-matrix $ \rho $, then the resulting state is $ u \, \rho \, u^\dagger $.

Use applyMatrix2() to left-multiply a non-unitary ComplexMatrix2

See also


Parameters
[in,out]quregobject representing the set of all qubits
[in]targetQubitqubit to operate on
[in]uunitary matrix to apply
Exceptions
invalidQuESTInputError()
  • if targetQubit is outside [0, qureg.numQubitsRepresented)
  • if matrix u is not unitary
Author
Ania Brown (state-vector)
Tyson Jones (density matrix, doc)

Definition at line 348 of file QuEST.c.

348  {
349  validateTarget(qureg, targetQubit, __func__);
350  validateOneQubitUnitaryMatrix(u, __func__);
351 
352  statevec_unitary(qureg, targetQubit, u);
353  if (qureg.isDensityMatrix) {
354  statevec_unitary(qureg, targetQubit+qureg.numQubitsRepresented, getConjugateMatrix2(u));
355  }
356 
357  qasm_recordUnitary(qureg, u, targetQubit);
358 }

References getConjugateMatrix2(), Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordUnitary(), statevec_unitary(), validateOneQubitUnitaryMatrix(), and validateTarget().

Referenced by TEST_CASE().

statevec_phaseShift
void statevec_phaseShift(Qureg qureg, int targetQubit, qreal angle)
Definition: QuEST_common.c:254
validateMultiControlsTarget
void validateMultiControlsTarget(Qureg qureg, int *controlQubits, int numControlQubits, int targetQubit, const char *caller)
Definition: QuEST_validation.c:452
statevec_sGate
void statevec_sGate(Qureg qureg, int targetQubit)
Definition: QuEST_common.c:268
statevec_pauliZ
void statevec_pauliZ(Qureg qureg, int targetQubit)
Definition: QuEST_common.c:261
pauliOpType
pauliOpType
Codes for specifying Pauli operators.
Definition: QuEST.h:96
statevec_rotateX
void statevec_rotateX(Qureg qureg, int rotQubit, qreal angle)
Definition: QuEST_common.c:296
validateTarget
void validateTarget(Qureg qureg, int targetQubit, const char *caller)
Definition: QuEST_validation.c:400
twoQubitUnitary
void twoQubitUnitary(Qureg qureg, int targetQubit1, int targetQubit2, ComplexMatrix4 u)
Apply a general two-qubit unitary (including a global phase factor).
Definition: QuEST.c:256
PAULI_Z
@ PAULI_Z
Definition: QuEST.h:96
statevec_multiControlledMultiRotatePauli
void statevec_multiControlledMultiRotatePauli(Qureg qureg, long long int ctrlMask, int *targetQubits, enum pauliOpType *targetPaulis, int numTargets, qreal angle, int applyConj)
Definition: QuEST_common.c:453
qasm_recordParamGate
void qasm_recordParamGate(Qureg qureg, TargetGate gate, int targetQubit, qreal param)
Definition: QuEST_qasm.c:187
shiftIndices
void shiftIndices(int *indices, int numIndices, int shift)
Definition: QuEST_common.c:156
statevec_controlledTwoQubitUnitary
void statevec_controlledTwoQubitUnitary(Qureg qureg, int controlQubit, int targetQubit1, int targetQubit2, ComplexMatrix4 u)
Definition: QuEST_common.c:567
PAULI_I
@ PAULI_I
Definition: QuEST.h:96
GATE_T
@ GATE_T
Definition: QuEST_qasm.h:24
GATE_PHASE_SHIFT
@ GATE_PHASE_SHIFT
Definition: QuEST_qasm.h:32
qasm_recordUnitary
void qasm_recordUnitary(Qureg qureg, ComplexMatrix2 u, int targetQubit)
Definition: QuEST_qasm.c:208
qasm_recordMultiControlledGate
void qasm_recordMultiControlledGate(Qureg qureg, TargetGate gate, int *controlQubits, int numControlQubits, int targetQubit)
Definition: QuEST_qasm.c:317
validateMultiQubitMatrixFitsInNode
void validateMultiQubitMatrixFitsInNode(Qureg qureg, int numTargets, const char *caller)
Definition: QuEST_validation.c:473
statevec_twoQubitUnitary
void statevec_twoQubitUnitary(Qureg qureg, int targetQubit1, int targetQubit2, ComplexMatrix4 u)
Definition: QuEST_common.c:561
statevec_tGateConj
void statevec_tGateConj(Qureg qureg, int targetQubit)
Definition: QuEST_common.c:289
statevec_unitary
void statevec_unitary(Qureg qureg, int targetQubit, ComplexMatrix2 u)
Definition: QuEST_cpu_distributed.c:895
getConjugateMatrix4
ComplexMatrix4 getConjugateMatrix4(ComplexMatrix4 src)
Definition: QuEST_common.c:110
GATE_ROTATE_X
@ GATE_ROTATE_X
Definition: QuEST_qasm.h:27
validateMultiQubitUnitaryMatrix
void validateMultiQubitUnitaryMatrix(Qureg qureg, ComplexMatrixN u, int numTargs, const char *caller)
Definition: QuEST_validation.c:502
statevec_multiControlledMultiQubitUnitary
void statevec_multiControlledMultiQubitUnitary(Qureg qureg, long long int ctrlMask, int *targs, int numTargs, ComplexMatrixN u)
This calls swapQubitAmps only when it would involve a distributed communication; if the qubit chunks ...
Definition: QuEST_cpu_distributed.c:1514
statevec_multiRotateZ
void statevec_multiRotateZ(Qureg qureg, long long int mask, qreal angle)
Definition: QuEST_cpu.c:3316
qasm_recordControlledCompactUnitary
void qasm_recordControlledCompactUnitary(Qureg qureg, Complex alpha, Complex beta, int controlQubit, int targetQubit)
Definition: QuEST_qasm.c:265
GATE_ROTATE_Z
@ GATE_ROTATE_Z
Definition: QuEST_qasm.h:29
GATE_SIGMA_Z
@ GATE_SIGMA_Z
Definition: QuEST_qasm.h:23
statevec_controlledPauliY
void statevec_controlledPauliY(Qureg qureg, int controlQubit, int targetQubit)
Definition: QuEST_cpu_distributed.c:1192
getConjugateScalar
Complex getConjugateScalar(Complex scalar)
Definition: QuEST_common.c:91
statevec_controlledPhaseShift
void statevec_controlledPhaseShift(Qureg qureg, int idQubit1, int idQubit2, qreal angle)
Definition: QuEST_cpu.c:3226
GATE_HADAMARD
@ GATE_HADAMARD
Definition: QuEST_qasm.h:26
getConjugateMatrix2
ComplexMatrix2 getConjugateMatrix2(ComplexMatrix2 src)
Definition: QuEST_common.c:105
statevec_multiControlledPhaseShift
void statevec_multiControlledPhaseShift(Qureg qureg, int *controlQubits, int numControlQubits, qreal angle)
Definition: QuEST_cpu.c:3266
statevec_pauliY
void statevec_pauliY(Qureg qureg, int targetQubit)
Definition: QuEST_cpu_distributed.c:1142
qasm_recordMultiControlledMultiQubitNot
void qasm_recordMultiControlledMultiQubitNot(Qureg qureg, int *ctrls, int numCtrls, int *targs, int numTargs)
Definition: QuEST_qasm.c:382
statevec_controlledMultiQubitUnitary
void statevec_controlledMultiQubitUnitary(Qureg qureg, int ctrl, int *targets, int numTargets, ComplexMatrixN u)
Definition: QuEST_common.c:579
multiRotatePauli
void multiRotatePauli(Qureg qureg, int *targetQubits, enum pauliOpType *targetPaulis, int numTargets, qreal angle)
Apply a multi-qubit multi-Pauli rotation, also known as a Pauli gadget, on a selected number of qubit...
Definition: QuEST.c:685
qasm_recordMultiStateControlledUnitary
void qasm_recordMultiStateControlledUnitary(Qureg qureg, ComplexMatrix2 u, int *controlQubits, int *controlState, int numControlQubits, int targetQubit)
Definition: QuEST_qasm.c:363
multiQubitUnitary
void multiQubitUnitary(Qureg qureg, int *targs, int numTargs, ComplexMatrixN u)
Apply a general multi-qubit unitary (including a global phase factor) with any number of target qubit...
Definition: QuEST.c:296
statevec_sqrtSwapGate
void statevec_sqrtSwapGate(Qureg qureg, int qb1, int qb2)
Definition: QuEST_common.c:387
PAULI_X
@ PAULI_X
Definition: QuEST.h:96
statevec_swapQubitAmps
void statevec_swapQubitAmps(Qureg qureg, int qb1, int qb2)
Definition: QuEST_cpu_distributed.c:1431
statevec_controlledPauliYConj
void statevec_controlledPauliYConj(Qureg qureg, int controlQubit, int targetQubit)
Definition: QuEST_cpu_distributed.c:1225
validateVector
void validateVector(Vector vec, const char *caller)
Definition: QuEST_validation.c:511
statevec_multiControlledMultiQubitNot
void statevec_multiControlledMultiQubitNot(Qureg qureg, int ctrlMask, int targMask)
Definition: QuEST_cpu_distributed.c:1097
validateMultiQubits
void validateMultiQubits(Qureg qureg, int *qubits, int numQubits, const char *caller)
Definition: QuEST_validation.c:444
statevec_controlledUnitary
void statevec_controlledUnitary(Qureg qureg, int controlQubit, int targetQubit, ComplexMatrix2 u)
Definition: QuEST_cpu_distributed.c:972
qasm_recordControlledGate
void qasm_recordControlledGate(Qureg qureg, TargetGate gate, int controlQubit, int targetQubit)
Definition: QuEST_qasm.c:239
multiControlledMultiRotatePauli
void multiControlledMultiRotatePauli(Qureg qureg, int *controlQubits, int numControls, int *targetQubits, enum pauliOpType *targetPaulis, int numTargets, qreal angle)
Apply a multi-controlled multi-target multi-Pauli rotation, also known as a controlled Pauli gadget.
Definition: QuEST.c:705
validateControlTarget
void validateControlTarget(Qureg qureg, int controlQubit, int targetQubit, const char *caller)
Definition: QuEST_validation.c:408
qasm_recordAxisRotation
void qasm_recordAxisRotation(Qureg qureg, qreal angle, Vector axis, int targetQubit)
Definition: QuEST_qasm.c:224
GATE_SQRT_SWAP
@ GATE_SQRT_SWAP
Definition: QuEST_qasm.h:34
statevec_multiControlledMultiRotateZ
void statevec_multiControlledMultiRotateZ(Qureg qureg, long long int ctrlMask, long long int targMask, qreal angle)
Definition: QuEST_cpu.c:3358
GATE_SIGMA_X
@ GATE_SIGMA_X
Definition: QuEST_qasm.h:21
statevec_tGate
void statevec_tGate(Qureg qureg, int targetQubit)
Definition: QuEST_common.c:275
validateControlState
void validateControlState(int *controlState, int numControlQubits, const char *caller)
Definition: QuEST_validation.c:468
validateMultiTargets
void validateMultiTargets(Qureg qureg, int *targetQubits, int numTargetQubits, const char *caller)
Definition: QuEST_validation.c:428
qasm_recordControlledParamGate
void qasm_recordControlledParamGate(Qureg qureg, TargetGate gate, int controlQubit, int targetQubit, qreal param)
Definition: QuEST_qasm.c:248
statevec_rotateAroundAxis
void statevec_rotateAroundAxis(Qureg qureg, int rotQubit, qreal angle, Vector axis)
Definition: QuEST_common.c:314
setConjugateMatrixN
void setConjugateMatrixN(ComplexMatrixN m)
Definition: QuEST_common.c:115
statevec_multiControlledTwoQubitUnitary
void statevec_multiControlledTwoQubitUnitary(Qureg qureg, long long int ctrlMask, int targetQubit1, int targetQubit2, ComplexMatrix4 u)
This calls swapQubitAmps only when it would involve a distributed communication; if the qubit chunks ...
Definition: QuEST_cpu_distributed.c:1458
qasm_recordControlledAxisRotation
void qasm_recordControlledAxisRotation(Qureg qureg, qreal angle, Vector axis, int controlQubit, int targetQubit)
Definition: QuEST_qasm.c:301
getQubitBitMask
long long int getQubitBitMask(int *qubits, int numQubits)
Definition: QuEST_common.c:50
statevec_compactUnitary
void statevec_compactUnitary(Qureg qureg, int targetQubit, Complex alpha, Complex beta)
Definition: QuEST_cpu_distributed.c:858
PAULI_Y
@ PAULI_Y
Definition: QuEST.h:96
statevec_multiRotatePauli
void statevec_multiRotatePauli(Qureg qureg, int *targetQubits, enum pauliOpType *targetPaulis, int numTargets, qreal angle, int applyConj)
applyConj=1 will apply conjugate operation, else applyConj=0
Definition: QuEST_common.c:414
statevec_multiControlledPhaseFlip
void statevec_multiControlledPhaseFlip(Qureg qureg, int *controlQubits, int numControlQubits)
Definition: QuEST_cpu.c:3718
qasm_recordComment
void qasm_recordComment(Qureg qureg, char *comment,...)
Definition: QuEST_qasm.c:121
statevec_multiQubitUnitary
void statevec_multiQubitUnitary(Qureg qureg, int *targets, int numTargets, ComplexMatrixN u)
Definition: QuEST_common.c:573
statevec_controlledRotateAroundAxis
void statevec_controlledRotateAroundAxis(Qureg qureg, int controlQubit, int targetQubit, qreal angle, Vector axis)
Definition: QuEST_common.c:330
statevec_sGateConj
void statevec_sGateConj(Qureg qureg, int targetQubit)
Definition: QuEST_common.c:282
statevec_rotateAroundAxisConj
void statevec_rotateAroundAxisConj(Qureg qureg, int rotQubit, qreal angle, Vector axis)
Definition: QuEST_common.c:321
getControlFlipMask
long long int getControlFlipMask(int *controlQubits, int *controlState, int numControlQubits)
Definition: QuEST_common.c:60
qasm_recordMultiControlledUnitary
void qasm_recordMultiControlledUnitary(Qureg qureg, ComplexMatrix2 u, int *controlQubits, int numControlQubits, int targetQubit)
additionally performs Rz on target to restore the global phase lost from u in QASM U(a,...
Definition: QuEST_qasm.c:342
qasm_recordMultiControlledParamGate
void qasm_recordMultiControlledParamGate(Qureg qureg, TargetGate gate, int *controlQubits, int numControlQubits, int targetQubit, qreal param)
Definition: QuEST_qasm.c:325
statevec_controlledNot
void statevec_controlledNot(Qureg qureg, int controlQubit, int targetQubit)
Definition: QuEST_cpu_distributed.c:1075
validateTwoQubitUnitaryMatrix
void validateTwoQubitUnitaryMatrix(Qureg qureg, ComplexMatrix4 u, const char *caller)
Definition: QuEST_validation.c:481
statevec_controlledRotateX
void statevec_controlledRotateX(Qureg qureg, int controlQubit, int targetQubit, qreal angle)
Definition: QuEST_common.c:346
Qureg::isDensityMatrix
int isDensityMatrix
Whether this instance is a density-state representation.
Definition: QuEST.h:325
statevec_hadamard
void statevec_hadamard(Qureg qureg, int targetQubit)
Definition: QuEST_cpu_distributed.c:1258
statevec_rotateY
void statevec_rotateY(Qureg qureg, int rotQubit, qreal angle)
Definition: QuEST_common.c:302
statevec_multiControlledUnitary
void statevec_multiControlledUnitary(Qureg qureg, long long int ctrlQubitsMask, long long int ctrlFlipMask, int targetQubit, ComplexMatrix2 u)
Definition: QuEST_cpu_distributed.c:1011
validateOneQubitUnitaryMatrix
void validateOneQubitUnitaryMatrix(ComplexMatrix2 u, const char *caller)
Definition: QuEST_validation.c:477
statevec_sqrtSwapGateConj
void statevec_sqrtSwapGateConj(Qureg qureg, int qb1, int qb2)
Definition: QuEST_common.c:400
statevec_controlledRotateZ
void statevec_controlledRotateZ(Qureg qureg, int controlQubit, int targetQubit, qreal angle)
Definition: QuEST_common.c:358
Qureg::numQubitsRepresented
int numQubitsRepresented
The number of qubits represented in either the state-vector or density matrix.
Definition: QuEST.h:327
statevec_pauliX
void statevec_pauliX(Qureg qureg, int targetQubit)
Definition: QuEST_cpu_distributed.c:1048
validateMultiControlsMultiTargets
void validateMultiControlsMultiTargets(Qureg qureg, int *controlQubits, int numControlQubits, int *targetQubits, int numTargetQubits, const char *caller)
Definition: QuEST_validation.c:459
GATE_S
@ GATE_S
Definition: QuEST_qasm.h:25
GATE_SWAP
@ GATE_SWAP
Definition: QuEST_qasm.h:33
statevec_controlledPhaseFlip
void statevec_controlledPhaseFlip(Qureg qureg, int idQubit1, int idQubit2)
Definition: QuEST_cpu.c:3687
GATE_SIGMA_Y
@ GATE_SIGMA_Y
Definition: QuEST_qasm.h:22
qasm_recordCompactUnitary
void qasm_recordCompactUnitary(Qureg qureg, Complex alpha, Complex beta, int targetQubit)
Definition: QuEST_qasm.c:196
qasm_recordControlledUnitary
void qasm_recordControlledUnitary(Qureg qureg, ComplexMatrix2 u, int controlQubit, int targetQubit)
additionally performs Rz on target to restore the global phase lost from u in QASM U(a,...
Definition: QuEST_qasm.c:279
statevec_controlledRotateY
void statevec_controlledRotateY(Qureg qureg, int controlQubit, int targetQubit, qreal angle)
Definition: QuEST_common.c:352
statevec_controlledRotateAroundAxisConj
void statevec_controlledRotateAroundAxisConj(Qureg qureg, int controlQubit, int targetQubit, qreal angle, Vector axis)
Definition: QuEST_common.c:337
qasm_recordGate
void qasm_recordGate(Qureg qureg, TargetGate gate, int targetQubit)
Definition: QuEST_qasm.c:179
validatePauliCodes
void validatePauliCodes(enum pauliOpType *pauliCodes, int numPauliCodes, const char *caller)
Definition: QuEST_validation.c:599
validateUnitaryComplexPair
void validateUnitaryComplexPair(Complex alpha, Complex beta, const char *caller)
Definition: QuEST_validation.c:507
GATE_ROTATE_Y
@ GATE_ROTATE_Y
Definition: QuEST_qasm.h:28
statevec_rotateZ
void statevec_rotateZ(Qureg qureg, int rotQubit, qreal angle)
Definition: QuEST_common.c:308
statevec_controlledCompactUnitary
void statevec_controlledCompactUnitary(Qureg qureg, int controlQubit, int targetQubit, Complex alpha, Complex beta)
Definition: QuEST_cpu_distributed.c:934
validateUniqueTargets
void validateUniqueTargets(Qureg qureg, int qubit1, int qubit2, const char *caller)
Definition: QuEST_validation.c:414
statevec_pauliYConj
void statevec_pauliYConj(Qureg qureg, int targetQubit)
Definition: QuEST_cpu_distributed.c:1167