Precision-agnostic types and data structures for representing numbers, quantum states, and operators. More...

Data Structures
struct	Complex
	Represents one complex number. More...

struct	ComplexMatrix2
	Represents a 2x2 matrix of complex numbers. More...

struct	ComplexMatrix4
	Represents a 4x4 matrix of complex numbers. More...

struct	ComplexMatrixN
	Represents a general 2^N by 2^N matrix of complex numbers. More...

struct	DiagonalOp
	Represents a diagonal complex operator on the full Hilbert state of a `Qureg`. More...

struct	PauliHamil
	A Pauli Hamiltonian, expressed as a real-weighted sum of pauli products, and which can hence represent any Hermitian operator. More...

struct	QuESTEnv
	Information about the environment the program is running in. More...

struct	Qureg
	Represents a system of qubits. More...

struct	Vector
	Represents a 3-vector of real numbers. More...

Macros
#define	fromComplex(comp) qcomp(comp.real, comp.imag)

#define	getStaticComplexMatrixN(numQubits, re, im)
	Creates a ComplexMatrixN struct which lives in the stack and so does not need freeing, but cannot be returned beyond the calling scope. More...

#define	qcomp

#define	qreal double

#define	QuEST_PREC 2

#define	toComplex(scalar) ((Complex) {.real = creal(scalar), .imag = cimag(scalar)})

Enumerations
enum	bitEncoding { UNSIGNED =0, TWOS_COMPLEMENT =1 }
	Flags for specifying how the bits in sub-register computational basis states are mapped to indices in functions like applyPhaseFunc(). More...

enum	pauliOpType { PAULI_I =0, PAULI_X =1, PAULI_Y =2, PAULI_Z =3 }
	Codes for specifying Pauli operators. More...

enum	phaseFunc { NORM =0, SCALED_NORM =1, INVERSE_NORM =2, SCALED_INVERSE_NORM =3, SCALED_INVERSE_SHIFTED_NORM =4, PRODUCT =5, SCALED_PRODUCT =6, INVERSE_PRODUCT =7, SCALED_INVERSE_PRODUCT =8, DISTANCE =9, SCALED_DISTANCE =10, INVERSE_DISTANCE =11, SCALED_INVERSE_DISTANCE =12, SCALED_INVERSE_SHIFTED_DISTANCE =13 }
	Flags for specifying named phase functions. More...

Functions
Qureg	createCloneQureg (Qureg qureg, QuESTEnv env)
	Create a new Qureg which is an exact clone of the passed qureg, which can be either a state-vector or a density matrix. More...

ComplexMatrixN	createComplexMatrixN (int numQubits)
	Allocate dynamic memory for a square complex matrix of any size, which can be passed to functions like multiQubitUnitary() and applyMatrixN(). More...

Qureg	createDensityQureg (int numQubits, QuESTEnv env)
	Creates a density matrix Qureg object representing a set of qubits which can enter noisy and mixed states. More...

DiagonalOp	createDiagonalOp (int numQubits, QuESTEnv env)
	Creates a DiagonalOp representing a diagonal operator on the full Hilbert space of a Qureg. More...

DiagonalOp	createDiagonalOpFromPauliHamilFile (char *fn, QuESTEnv env)
	Creates and initialiases a diagonal operator from the Z Pauli Hamiltonian encoded in file with filename `fn`. More...

PauliHamil	createPauliHamil (int numQubits, int numSumTerms)
	Dynamically allocates a Hamiltonian expressed as a real-weighted sum of products of Pauli operators. More...

PauliHamil	createPauliHamilFromFile (char *fn)
	Creates a `PauliHamil` instance, a real-weighted sum of products of Pauli operators, populated with the data in filename `fn`. More...

QuESTEnv	createQuESTEnv (void)
	Create the QuEST execution environment. More...

Qureg	createQureg (int numQubits, QuESTEnv env)
	Creates a state-vector Qureg object representing a set of qubits which will remain in a pure state. More...

void	destroyComplexMatrixN (ComplexMatrixN matr)
	Destroy a ComplexMatrixN instance created with createComplexMatrixN() More...

void	destroyDiagonalOp (DiagonalOp op, QuESTEnv env)
	Destroys a DiagonalOp created with createDiagonalOp(), freeing its memory. More...

void	destroyPauliHamil (PauliHamil hamil)
	Destroy a PauliHamil instance, created with either createPauliHamil() or createPauliHamilFromFile(). More...

void	destroyQuESTEnv (QuESTEnv env)
	Destroy the QuEST environment. More...

void	destroyQureg (Qureg qureg, QuESTEnv env)
	Deallocate a Qureg, freeing its memory. More...

void	initComplexMatrixN (ComplexMatrixN m, qreal real[][1<< m.numQubits], qreal imag[][1<< m.numQubits])
	Initialises a ComplexMatrixN instance to have the passed `real` and `imag` values. More...

void	initDiagonalOp (DiagonalOp op, qreal real, qreal imag)
	Overwrites the entire DiagonalOp `op` with the given `real` and `imag` complex elements. More...

void	initDiagonalOpFromPauliHamil (DiagonalOp op, PauliHamil hamil)
	Populates the diagonal operator `op` to be equivalent to the given Pauli Hamiltonian `hamil`, assuming `hamil` contains only `PAULI_Z` operators. More...

void	initPauliHamil (PauliHamil hamil, qreal coeffs, enum pauliOpType codes)
	Initialise PauliHamil instance `hamil` with the given term coefficients and Pauli codes (one for every qubit in every term). More...

void	setDiagonalOpElems (DiagonalOp op, long long int startInd, qreal real, qreal imag, long long int numElems)
	Modifies a subset (starting at index `startInd`, and ending at index `startInd` + `numElems`) of the elements in DiagonalOp `op` with the given complex numbers (passed as `real` and `imag` components). More...

void	syncDiagonalOp (DiagonalOp op)
	Update the GPU memory with the current values in `op.real` and `op.imag`. More...

Detailed Description

Precision-agnostic types and data structures for representing numbers, quantum states, and operators.

Macro Definition Documentation

◆ fromComplex

#define fromComplex ( comp ) qcomp(comp.real, comp.imag)

Converts a Complex struct to a qcomp native type

Author: Tyson Jones

◆ getStaticComplexMatrixN

#define getStaticComplexMatrixN	(	numQubits,
		re,
		im
	)

Value:

    bindArraysToStackComplexMatrixN( \
        numQubits, \
        (qreal[1<<numQubits][1<<numQubits]) UNPACK_ARR re, \
        (qreal[1<<numQubits][1<<numQubits]) UNPACK_ARR im, \
        (double*[1<<numQubits]) {NULL}, (double*[1<<numQubits]) {NULL} \
    )

Creates a ComplexMatrixN struct which lives in the stack and so does not need freeing, but cannot be returned beyond the calling scope.

That is, the .real and .imag arrays of the returned ComplexMatrixN live in the stack as opposed to that returned by createComplexMatrixN() (which live in the heap). Note the real and imag components must be wrapped in paranthesis, e.g.

ComplexMatrixN u = getStaticComplexMatrixN(1, ({{1,2},{3,4}}), ({{0}}));

Here is an example of an incorrect usage, since a 'local' ComplexMatrixN cannot leave the calling scope (otherwise inducing dangling pointers):

ComplexMatrixN getMyMatrix(void) {
    return getStaticComplexMatrixN(1, ({{1,2},{3,4}}), ({{0}}));
}

This function is actually a single-line anonymous macro, so can be safely invoked within arguments to other functions, e.g.

multiQubitUnitary(
    qureg, (int[]) {0}, 1, 
    getStaticComplexMatrixN(1, ({{1,0},{0,1}}), ({{0}}))
);

The returned ComplexMatrixN can be accessed and modified in the same way as that returned by createComplexMatrixN(), e.g.

ComplexMatrixN u = getStaticComplexMatrixN(3, ({{0}}), ({{0}}));
for (int i=0; i<8; i++)
    for (int j=0; j<8; j++)
        u.real[i][j] = .1;

Note that the first argument numQubits must be a literal.

This macro is only callable in C, since it invokes the function bindArraysToStackComplexMatrixN() which is only callable in C.

See also

createComplexMatrixN()

Author: Tyson Jones

Definition at line 5521 of file QuEST.h.

◆ qcomp

#define qcomp

A precision-agnostic operator-overloaded complex number type.
This is a complex analog of qreal and is of single, double or quad precision depending on the value of QuEST_PREC. It resolves to the native complex type provided by <complex.h> for both C99 and C++11, so can be used with operators. It can be constructed with qcomp(real, imag).

For example, in C,

qcomp x = 2 + 3i;

x -= 3.2*x;

and in C++,

qcomp x = qcomp(2, 3);

x -= 3*x;

Assuming QuEST_PREC=4, qcomp will be 'complex long double' in C and 'complex<long double>' in C++.

Can be converted to/from Complex, the struct accepted by the QuEST interface, using toComplex and fromComplex.

Authors: Randy Meyers and Dr. Thomas Plum (created C & C++ agnosticism)

Author: Tyson Jones (created precision agnosticism)

◆ qreal

#define qreal double

A precision-agnostic floating point number, as determined by QuEST_PREC. Is a single, double or quad precision float when QuEST_PREC is 1, 2 or 4 respectively.

Author: Ania Brown; Tyson Jones (doc)

◆ QuEST_PREC

#define QuEST_PREC 2

Sets the precision of qreal and qcomp floating-point numbers, and hence the numerical precision of Qureg.

QuEST_PREC can be set as a preprocessor macro during compilation, or by editing its definition in QuEST_precision.h.
The possible values are:

QuEST_PREC	qreal	sizeof(qreal)
1	`float`	4 bytes
2	`double`	8 bytes
4	`long double`	16 bytes

Note that quad precision (QuEST_PREC = 4 ) is not compatible with most GPUs.

See also

createQureg() and createDensityQureg() for the total memory costs of creating registers under these precisions.

Author: Ania Brown; Tyson Jones (doc)

◆ toComplex

#define toComplex ( scalar ) ((Complex) {.real = creal(scalar), .imag = cimag(scalar)})

Creates a Complex struct, which can be passed to the QuEST API, from a qcomp

Author: Tyson Jones

Enumeration Type Documentation

◆ bitEncoding

enum bitEncoding

Flags for specifying how the bits in sub-register computational basis states are mapped to indices in functions like applyPhaseFunc().

UNSIGNED means the bits encode an unsigned integer, hence
$\begin{aligned} |00\rangle & \rightarrow \, 0 \\ |01\rangle & \rightarrow \, 1 \\ |10\rangle & \rightarrow \, 2 \\ |11\rangle & \rightarrow \, 3 \end{aligned}$
TWOS_COMPLEMENT means the bits encode a signed integer through two's complement, such that
$\begin{aligned} |000\rangle & \rightarrow \, 0 \\ |001\rangle & \rightarrow \, 1 \\ |010\rangle & \rightarrow \, 2 \\ |011\rangle & \rightarrow \, 3 \\ |100\rangle & \rightarrow \,-4 \\ |101\rangle & \rightarrow \,-3 \\ |110\rangle & \rightarrow \,-2 \\ |111\rangle & \rightarrow \,-1 \end{aligned}$

Remember that the qubits specified within a sub-register, and their ordering (least to most significant) determine the bits of a computational basis state, before intrepretation as an encoding of an integer.

Author: Tyson Jones

Enumerator
UNSIGNED
TWOS_COMPLEMENT

Definition at line 269 of file QuEST.h.

269 {UNSIGNED=0, TWOS_COMPLEMENT=1};

◆ pauliOpType

enum pauliOpType

Codes for specifying Pauli operators.

Author: Tyson Jones

Enumerator
PAULI_I
PAULI_X
PAULI_Y
PAULI_Z

Definition at line 96 of file QuEST.h.

96 {PAULI_I=0, PAULI_X=1, PAULI_Y=2, PAULI_Z=3};

◆ phaseFunc

enum phaseFunc

Flags for specifying named phase functions.

These can be passed to functions applyNamedPhaseFunc(), applyNamedPhaseFuncOverrides(), applyParamNamedPhaseFunc(), and applyParamNamedPhaseFuncOverrides().

Norm based phase functions:

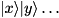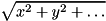
NORM maps state $|x\rangle|y\rangle\dots$ to $\sqrt{x^2 + y^2 + \dots}$
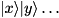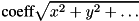
SCALED_NORM maps state $|x\rangle|y\rangle\dots$ to $\text{coeff} \sqrt{x^2 + y^2 + \dots}$
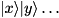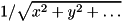
INVERSE_NORM maps state $|x\rangle|y\rangle\dots$ to $1/\sqrt{x^2 + y^2 + \dots}$
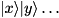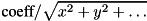
SCALED_INVERSE_NORM maps state $|x\rangle|y\rangle\dots$ to $\text{coeff}/\sqrt{x^2 + y^2 + \dots}$
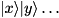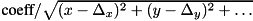
SCALED_INVERSE_SHIFTED_NORM maps state $|x\rangle|y\rangle\dots$ to $\text{coeff}/\sqrt{(x-\Delta_x)^2 + (y-\Delta_y)^2 + \dots}$

Product based phase functions:

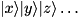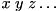
PRODUCT maps state $|x\rangle|y\rangle|z\rangle\dots$ to $x \; y \; z \dots$
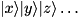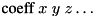
SCALED_PRODUCT maps state $|x\rangle|y\rangle|z\rangle\dots$ to $\text{coeff} \; x \; y \; z \dots$
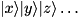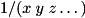
INVERSE_PRODUCT maps state $|x\rangle|y\rangle|z\rangle\dots$ to $1/(x \; y \; z \dots)$
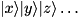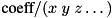
SCALED_INVERSE_PRODUCT maps state $|x\rangle|y\rangle|z\rangle\dots$ to $\text{coeff}/(x \; y \; z \dots)$

Euclidean distance based phase functions:

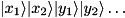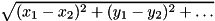
DISTANCE maps state $|x_1\rangle|x_2\rangle|y_1\rangle|y_2\rangle\dots$ to $\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 + \dots}$
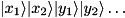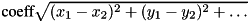
SCALED_DISTANCE maps state $|x_1\rangle|x_2\rangle|y_1\rangle|y_2\rangle\dots$ to $\text{coeff}\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 + \dots}$
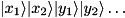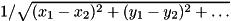
INVERSE_DISTANCE maps state $|x_1\rangle|x_2\rangle|y_1\rangle|y_2\rangle\dots$ to $1/\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 + \dots}$
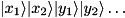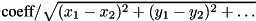
SCALED_INVERSE_DISTANCE maps state $|x_1\rangle|x_2\rangle|y_1\rangle|y_2\rangle\dots$ to $\text{coeff}/\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 + \dots}$
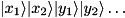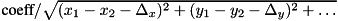
SCALED_INVERSE_SHIFTED_DISTANCE maps state $|x_1\rangle|x_2\rangle|y_1\rangle|y_2\rangle\dots$ to $\text{coeff}/\sqrt{(x_1-x_2-\Delta_x)^2 + (y_1-y_2-\Delta_y)^2 + \dots}$

Author: Tyson Jones; Richard Meister (shifted functions)

Enumerator
NORM
SCALED_NORM
INVERSE_NORM
SCALED_INVERSE_NORM
SCALED_INVERSE_SHIFTED_NORM
PRODUCT
SCALED_PRODUCT
INVERSE_PRODUCT
SCALED_INVERSE_PRODUCT
DISTANCE
SCALED_DISTANCE
INVERSE_DISTANCE
SCALED_INVERSE_DISTANCE
SCALED_INVERSE_SHIFTED_DISTANCE

Definition at line 231 of file QuEST.h.

                {
     NORM=0,     SCALED_NORM=1,      INVERSE_NORM=2,      SCALED_INVERSE_NORM=3,      SCALED_INVERSE_SHIFTED_NORM=4,
     PRODUCT=5,  SCALED_PRODUCT=6,   INVERSE_PRODUCT=7,   SCALED_INVERSE_PRODUCT=8,
     DISTANCE=9, SCALED_DISTANCE=10, INVERSE_DISTANCE=11, SCALED_INVERSE_DISTANCE=12, SCALED_INVERSE_SHIFTED_DISTANCE=13};

Function Documentation

◆ createCloneQureg()

Qureg createCloneQureg	(	Qureg	qureg,
		QuESTEnv	env
	)

Create a new Qureg which is an exact clone of the passed qureg, which can be either a state-vector or a density matrix.

The returned Qureg will have the same dimensions as the passed qureg and begin in an identical quantum state. This must be destroyed by the user later with destroyQureg().

See also

Returns: an object representing the set of qubits

Parameters

[in]	qureg	an existing Qureg to be cloned
[in]	env	the QuESTEnv

Author: Tyson Jones

Definition at line 64 of file QuEST.c.

                                                   {
  
     Qureg newQureg;
     statevec_createQureg(&newQureg, qureg.numQubitsInStateVec, env);
     newQureg.isDensityMatrix = qureg.isDensityMatrix;
     newQureg.numQubitsRepresented = qureg.numQubitsRepresented;
     newQureg.numQubitsInStateVec = qureg.numQubitsInStateVec;
     
     qasm_setup(&newQureg);
     statevec_cloneQureg(newQureg, qureg);
     return newQureg;
 }

References Qureg::isDensityMatrix, Qureg::numQubitsInStateVec, Qureg::numQubitsRepresented, qasm_setup(), statevec_cloneQureg(), and statevec_createQureg().

Referenced by TEST_CASE().

◆ createComplexMatrixN()

ComplexMatrixN createComplexMatrixN ( int numQubits )

Allocate dynamic memory for a square complex matrix of any size, which can be passed to functions like multiQubitUnitary() and applyMatrixN().

The returned matrix will have dimensions

$2^{\text{numQubits}} \times 2^{\text{numQubits}},$

stored as nested arrays ComplexMatrixN.real and ComplexMatrixN.imag, initialised to zero.

Unlike a Qureg, the memory of a ComplexMatrixN is always stored in RAM, and non-distributed. Hence, elements can be directly accessed and modified:

int numQubits = 5;
int dim = (1 << numQubits);
ComplexMatrixN m = createComplexMatrixN(numQubits);
 
for (int r=0; r<dim; r++) {
    for (int c=0; c<dim; c++) {
        m.real[r][c] = rand();
        m.imag[r][c] = rand();
    }
}

A ComplexMatrixN can be initialised in bulk using initComplexMatrixN(), though this is not C++ compatible.

Like ComplexMatrix2 and ComplexMatrix4 (which are incidentally stored in the stack), the returned ComplexMatrixN is safe to return from functions.

The ComplexMatrixN must eventually be freed using destroyComplexMatrixN(), since it is created in the dynamic heap. One can instead use getStaticComplexMatrixN() to create a ComplexMatrixN struct in the stack (which doesn't need to be later destroyed), though this may cause a stack overflow if the matrix is too large (approx 10+ qubits).

See also

Parameters

[in] numQubits the number of qubits of which the returned ComplexMatrixN will correspond

Returns: a dynamic ComplexMatrixN struct, that is one where the .real and .imag fields are arrays kept in the heap and must be later destroyed.

Exceptions

invalidQuESTInputError()

if numQubits <= 0
if the memory was not allocated successfully

Author: Tyson Jones

Definition at line 1348 of file QuEST.c.

                                                     {
      validateNumQubitsInMatrix(numQubits, __func__);
  
      int numRows = 1 << numQubits;
  
      ComplexMatrixN m = {
          .numQubits = numQubits,
          .real = malloc(numRows * sizeof *m.real),
          .imag = malloc(numRows * sizeof *m.imag)};
  
      for (int n=0; n < 1<<numQubits; n++) {
          m.real[n] = calloc(numRows, sizeof **m.real);
          m.imag[n] = calloc(numRows, sizeof **m.imag);
      }
      
      // error if the ComplexMatrixN was not successfully malloc'ds
      validateMatrixInit(m, __func__);
      
      return m;
  }

References ComplexMatrixN::imag, ComplexMatrixN::numQubits, ComplexMatrixN::real, validateMatrixInit(), and validateNumQubitsInMatrix().

Referenced by densmatr_mixMultiQubitKrausMap(), densmatr_mixTwoQubitKrausMap(), and TEST_CASE().

◆ createDensityQureg()

Qureg createDensityQureg	(	int	numQubits,
		QuESTEnv	env
	)

Creates a density matrix Qureg object representing a set of qubits which can enter noisy and mixed states.

Allocates space for a matrix of complex amplitudes, which assuming a single qreal floating-point number requires qrealBytes, requires memory

$\text{qrealBytes} \times 2 \times 2^{2 \times\text{numQubits}}\;\;\text{(bytes)},$

though there are additional memory costs in GPU and distributed modes. Notice this is the memory cost of a state-vector created with createQureg() of twice as many qubits.

The returned Qureg begins in the zero state, as produced by initZeroState().

Once created, the following Qureg fields are relevant in all backends:

Behind the scenes, density matrice are stored as state-vectors, flattened column-wise. As such, individual amplitudes should be fetched with getDensityAmp(), in lieu of direct access.

QuESTEnv env must be prior created with createQuESTEnv().

Serial

In serial and local (non-distributed) multithreaded modes, a density matrix Qureg costs only the memory above. For example, at double precision (QuEST_PREC = 2, qrealBytes = 8), the memory costs are:

`numQubits`	memory
10	16 MiB
12	256 MiB
14	4 GiB
16	64 GiB
18	1 TiB
20	16 TiB

GPU

In GPU-accelerated mode, an additional density matrix is created in GPU memory. Therefore both RAM and VRAM must be of sufficient memory to store the state-vector, each of the size indicated in the Serial table above.

Note that many GPUs do not support quad precision qreal.

Distributed

In distributed mode, the density matrix is uniformly partitioned between the N distributed nodes (column-wise).

Only a power-of-2 number of nodes N may be used (e.g. N = 1, 2, 4, 8, ...). There must additionally be at least 1 amplitude of a density matrix stored on each node. This means one cannot create a density matrix Qureg with fewer than $\log_2(\text{N})/2$ qubits.

Additional memory is allocated on each node for communication buffers, of size equal to the density matrix partition. Hence the total memory per-node required is:

$2 \times \text{qrealBytes} \times 2 \times 2^{2\times\text{numQubits}}/N \;\;\text{(bytes)},$

For example, at double precision (QuEST_PREC = 2, qrealBytes = 8), the memory costs are:

`numQubits`	memory per node
	N = 2	N = 4	N = 8	N = 16	N = 32
10	16 MiB	8 MiB	4 MiB	2 MiB	1 MiB
15	16 GiB	8 GiB	4 GiB	2 GiB	1 GiB
20	16 TiB	8 TiB	4 TiB	2 TiB	1 TiB

See also

createQureg() to create a state-vector of the equivalent number of qubits, with a square-root memory cost
createCloneQureg() to create a new qureg of the size and state of an existing qureg.
destroyQureg() to free the allocated Qureg memory.
reportQuregParams() to print information about a Qureg.

Returns: an object representing the set of qubits

Parameters

[in]	numQubits	number of qubits in the system
[in]	env	object representing the execution environment (local, multinode etc)

Exceptions

invalidQuESTInputError()	if `numQubits` <= 0 if `numQubits` is so large that the number of amplitudes cannot fit in a long long int type, if in distributed mode, there are more nodes than elements in the would-be state-vector
exit	if in GPU mode, but GPU memory cannot be allocated.

Author: Tyson Jones

Definition at line 50 of file QuEST.c.

                                                       {
     validateNumQubitsInQureg(2*numQubits, env.numRanks, __func__);
     
     Qureg qureg;
     statevec_createQureg(&qureg, 2*numQubits, env);
     qureg.isDensityMatrix = 1;
     qureg.numQubitsRepresented = numQubits;
     qureg.numQubitsInStateVec = 2*numQubits;
     
     qasm_setup(&qureg);
     initZeroState(qureg); // safe call to public function
     return qureg;
 }

References initZeroState(), Qureg::isDensityMatrix, Qureg::numQubitsInStateVec, Qureg::numQubitsRepresented, QuESTEnv::numRanks, qasm_setup(), statevec_createQureg(), and validateNumQubitsInQureg().

Referenced by TEST_CASE().

◆ createDiagonalOp()

DiagonalOp createDiagonalOp	(	int	numQubits,
		QuESTEnv	env
	)

Creates a DiagonalOp representing a diagonal operator on the full Hilbert space of a Qureg.

The resulting operator need not be unitary nor Hermitian, and can be applied to any Qureg of a compatible number of qubits.

This function allocates space for 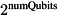$2^{\text{numQubits}}$ complex amplitudes, which are initially zero. This is the same cost as a local state-vector of equal number of qubits; see the Serial section of createQureg(). Note that this is a paralell data-type, so its ultimate memory costs depend on the hardware backends, as elaborated below.

The operator elements should be modified with initDiagonalOp() and setDiagonalOpElems(), and must be later freed with destroyDiagonalOp().

GPU

In GPU-accelerated mode, this function also creates additional equally-sized persistent memory on the GPU. If you wish to modify the operator elements directly (in lieu of setDiagonalOpElems()), you must thereafter call syncDiagonalOp() to update the operator stored in VRAM.

For example,

DiagonalOp op = createDiagonalOp(4, env);
for (long long int i=0; i<op.numElemsPerChunk; i++) {
    op.real[i] = rand();
    op.imag[i] = rand();
}
syncDiagonalOp(op);

Distribution

In distributed mode, the memory for the diagonal operator is divided evenly between the 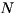$N$ available nodes, such that each node contains only 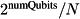$2^{\text{numQubits}}/N$ complex values. This is assigned to DiagonalOp.numElemsPerChunk.

Users must therefore exercise care in modifying DiagonalOp.real and DiagonalOp.imag directly.

For example, the following is valid code when when distributed between N = 2 nodes:

// create diag({1,2,3,4,5,6,7,8, 9,10,11,12,13,14,15,16})
int numQubits = 4;
DiagonalOp op = createDiagonalOp(numQubits4, env);
for (int i=0; i<8; i++) {
    if (env.rank == 0)
        op.real[i] = (i+1);
    if (env.rank == 1)
        op.real[i] = (i+1+8);
}

See also

Returns: a dynamic DiagonalOp instance initialised to diag(0,0,...).

Parameters

[in]	numQubits	number of qubits which inform the Hilbert dimension of the operator.
[in]	env	the QuESTEnv

Exceptions

invalidQuESTInputError()	if `numQubits` <= 0 if `numQubits` is so large that the number of elements cannot fit in a long long int type, if in distributed mode, there are more nodes than elements in the operator
exit	if the memory could not be allocated

Author: Tyson Jones

Definition at line 1518 of file QuEST.c.

                                                          {
     validateNumQubitsInDiagOp(numQubits, env.numRanks, __func__);
     
     return agnostic_createDiagonalOp(numQubits, env);
 }

References agnostic_createDiagonalOp(), QuESTEnv::numRanks, and validateNumQubitsInDiagOp().

Referenced by TEST_CASE().

◆ createDiagonalOpFromPauliHamilFile()

DiagonalOp createDiagonalOpFromPauliHamilFile	(	char *	fn,
		QuESTEnv	env
	)

Creates and initialiases a diagonal operator from the Z Pauli Hamiltonian encoded in file with filename fn.

This is a convenience function to prepare a diagonal operator from a plaintext description of an all-Z Pauli Hamiltonian. The returned DiagonalOp is a distributed data structure, and significantly faster to use (through functions like calcExpecDiagonalOp()) than PauliHamil functions (like calcExpecPauliHamil()).

See createDiagonalOp() for info about the returned operator.
See initDiagonalOpFromPauliHamil() for info about the initialised state.
See createPauliHamilFromFile() for info about the required file format.

The returned DiagonalOp must be later freed with destroyDiagonalOp().
Note a PauliHamil from fn is temporarily internally created.

This function is equivalent to

// produce diagonal matrix d
PauliHamil h = createPauliHamilFromFile(fn);
DiagonalOp d = createDiagonalOp(h.numQubits, env);
initDiagonalOpFromPauliHamil(d, h); 
destroyPauliHamil(h);

See also

Parameters

[in]	fn	filename of a plaintext file encoding an all-Z Pauli Hamiltonian
[in]	env	the session QuESTEnv

Returns: a created DiagonalOp equivalent to the Hamiltonian in fn

Exceptions

invalidQuESTInputError()

if file fn cannot be read
if file fn does not encode a valid PauliHamil
if the encoded PauliHamil consists of operators other than PAULI_Z and PAULI_I

Author: Tyson Jones; Milos Prokop (serial prototype)

Definition at line 1558 of file QuEST.c.

                                                                       {
     PauliHamil h = createPauliHamilFromFile(fn); // validates fn
     validateDiagPauliHamilFromFile(h, env.numRanks, __func__);  // destroys h if invalid
  
     DiagonalOp op = agnostic_createDiagonalOp(h.numQubits, env);
     agnostic_initDiagonalOpFromPauliHamil(op, h);
     
     destroyPauliHamil(h);
     return op;
 }

References agnostic_createDiagonalOp(), agnostic_initDiagonalOpFromPauliHamil(), createPauliHamilFromFile(), destroyPauliHamil(), PauliHamil::numQubits, QuESTEnv::numRanks, and validateDiagPauliHamilFromFile().

Referenced by TEST_CASE().

◆ createPauliHamil()

PauliHamil createPauliHamil	(	int	numQubits,
		int	numSumTerms
	)

Dynamically allocates a Hamiltonian expressed as a real-weighted sum of products of Pauli operators.

A PauliHamil is merely an encapsulation of the multiple parameters of functions like applyPauliSum().

The Pauli operators (PauliHamil.pauliCodes) are all initialised to identity (PAULI_I), but the coefficients (PauliHamil.termCoeffs) are not initialised.

The Hamiltonian can be used in functions like applyPauliHamil() and applyTrotterCircuit(), with Qureg instances of the same number of qubits.

A PauliHamil can be modified directly (see PauliHamil), or through initPauliHamil(). It can furthermore be created and initialised from a file description directly with createPauliHamilFromFile().

The returned dynamic PauliHamil instance must later be freed via destroyPauliHamil().

See also

Parameters

[in]	numQubits	the number of qubits on which this Hamiltonian acts
[in]	numSumTerms	the number of weighted terms in the sum, or the number of Pauli products

Returns: a dynamic PauliHamil struct, with fields pauliCodes and termCoeffs stored in the heap

Exceptions

invalidQuESTInputError()

if numQubits <= 0
if numSumTerms <= 0

Author: Tyson Jones

Definition at line 1398 of file QuEST.c.

                                                             {
     validateHamilParams(numQubits, numSumTerms, __func__);
     
     PauliHamil h;
     h.numQubits = numQubits;
     h.numSumTerms = numSumTerms;
     h.termCoeffs = malloc(numSumTerms * sizeof *h.termCoeffs);
     h.pauliCodes = malloc(numQubits*numSumTerms * sizeof *h.pauliCodes);
     
     // initialise pauli codes to identity 
     for (int i=0; i<numQubits*numSumTerms; i++)
         h.pauliCodes[i] = PAULI_I;
     
     return h;
 }

References PauliHamil::numQubits, PauliHamil::numSumTerms, PAULI_I, PauliHamil::pauliCodes, PauliHamil::termCoeffs, and validateHamilParams().

Referenced by createPauliHamilFromFile(), and TEST_CASE().

◆ createPauliHamilFromFile()

PauliHamil createPauliHamilFromFile ( char * fn )

Creates a PauliHamil instance, a real-weighted sum of products of Pauli operators, populated with the data in filename fn.

Each line in the plaintext file is interpreted as a separate product of Pauli operators in the total sum. Each line must be a space-separated list with format

c p1 p2 p3 ... pN

where c is the real coefficient of the term, and p1 ... pN are numbers in {0,1,2,3} to indicate PAULI_I, PAULI_X, PAULI_Y, PAULI_Z operators respectively, which act on qubits 0 through N-1 (all qubits).

For example, the file containing

0.31 1 0 1 2
-0.2 3 2 0 0

encodes a two-term four-qubit Hamiltonian

$0.31 \, X_0 \, X_2 \, Y_3 -0.2 \, Z_0 \, Y_1 \,.$

The initialised PauliHamil can be previewed with reportPauliHamil().

The number of qubits and terms are inferred from the file. The created Hamiltonian can be used just like one created via createPauliHamil(). It can be modified directly (see PauliHamil), or through initPauliHamil().

The returned dynamic PauliHamil instance must later be freed via destroyPauliHamil().

See also

Parameters

[in] fn filename of the plaintext file specifying the pauli operators and coefficients

Returns: a dynamic PauliHamil struct

Exceptions

invalidQuESTInputError()

if the file with name fn cannot be read
if the file is not correctly formatted as described above

Author: Tyson Jones

Definition at line 1420 of file QuEST.c.

                                               {
     
     /* The validation in this function must close the file handle and free 
      * allocated memory before raising an error (whether that's a C exit, or
      * an overriden C++ exception).
      */
     
         FILE* file = fopen(fn, "r");
     int success = (file != NULL);
     validateFileOpened(success, fn, __func__);
     
     /* file format: coeff {term} \n where {term} is #numQubits values of 
          * 0 1 2 3 signifying I X Y Z acting on that qubit index
          */
         
         // count the number of qubits (ignore trailing whitespace)
         int numQubits = -1; // to exclude coeff at start
         char ch = getc(file);
     char prev = '0'; // anything not space
         while (ch != '\n' && ch != EOF) {
                 if (ch == ' ' && prev != ' ') // skip multiple spaces
                         numQubits++;
         prev = ch;
         ch = getc(file);
     }
     // edge-case: if we hit EOF/newline without a space
     if (prev != ' ')
         numQubits++;
  
     /* TODO:
      * The below code may break on Windows where newlines are multiple characters
      */
         
         // count the number of terms (being cautious of trailing newlines)
     int numTerms = 0;
     prev = '\n';
     rewind(file);
         while ((ch=getc(file)) != EOF) {
                 if (ch == '\n' && prev != '\n')
                         numTerms++;
         prev = ch;
     }
     // edge-case: if we hit EOF without a newline, count that line
     if (prev != '\n')
         numTerms++;
  
     // validate the inferred number of terms and qubits (closes file if error)
     validateHamilFileParams(numQubits, numTerms, file, fn, __func__);
     
     // allocate space for PauliHamil data
     PauliHamil h = createPauliHamil(numQubits, numTerms);
      
     // specifier for a qreal number then a space 
     char strSpec[50];
     strcpy(strSpec, REAL_SPECIFIER);
     strcat(strSpec, " ");
     
     // collect coefficients and terms
         rewind(file);
         for (int t=0; t<numTerms; t++) {
                 
                 // record coefficient, and validate (closes file and frees h if error)
         success = fscanf(file, strSpec, &(h.termCoeffs[t])) == 1;
         validateHamilFileCoeffParsed(success, h, file, fn, __func__);
  
                 // record Pauli operations, and validate (closes file and frees h if error)
         for (int q=0; q<numQubits; q++) {
             int i = t*numQubits + q;
             
             // verbose, to avoid type warnings
             int code;
             success = fscanf(file, "%d ", &code) == 1;
             h.pauliCodes[i] = (enum pauliOpType) code;
             validateHamilFilePauliParsed(success, h, file, fn, __func__);
             validateHamilFilePauliCode(h.pauliCodes[i], h, file, fn, __func__);
                 }
  
                 // the trailing newline is magically eaten
         }
  
     fclose(file);
         return h;
 }

References createPauliHamil(), PauliHamil::pauliCodes, PauliHamil::termCoeffs, validateFileOpened(), validateHamilFileCoeffParsed(), validateHamilFileParams(), validateHamilFilePauliCode(), and validateHamilFilePauliParsed().

Referenced by createDiagonalOpFromPauliHamilFile(), and TEST_CASE().

◆ createQuESTEnv()

QuESTEnv createQuESTEnv ( void )

Create the QuEST execution environment.

This should be called only once, and the environment should be freed with destroyQuESTEnv at the end of the user's code. If something needs to be done to set up the execution environment, such as initializing MPI when running in distributed mode, it is handled here.

See also

Returns: object representing the execution environment. A single instance is used for each program

Author: Ania Brown

Definition at line 129 of file QuEST_cpu_distributed.c.

                               {
     
     QuESTEnv env;
     
     // init MPI environment
     int rank, numRanks, initialized;
     MPI_Initialized(&initialized);
     if (!initialized){
         MPI_Init(NULL, NULL);
         MPI_Comm_size(MPI_COMM_WORLD, &numRanks);
         MPI_Comm_rank(MPI_COMM_WORLD, &rank);
  
         env.rank=rank;
         env.numRanks=numRanks;
  
     } else {
         
         printf("ERROR: Trying to initialize QuESTEnv multiple times. Ignoring...\n");
         
         // ensure env is initialised anyway, so the compiler is happy
         MPI_Comm_size(MPI_COMM_WORLD, &numRanks);
         MPI_Comm_rank(MPI_COMM_WORLD, &rank);
         env.rank=rank;
         env.numRanks=numRanks;
         }
     
     validateNumRanks(env.numRanks, __func__);
     
     env.seeds = NULL;
     env.numSeeds = 0;
         seedQuESTDefault(&env);
     
     return env;
 }

References GPUExists(), QuESTEnv::numRanks, QuESTEnv::numSeeds, QuESTEnv::rank, seedQuESTDefault(), QuESTEnv::seeds, and validateNumRanks().

Referenced by main().

◆ createQureg()

Qureg createQureg	(	int	numQubits,
		QuESTEnv	env
	)

Creates a state-vector Qureg object representing a set of qubits which will remain in a pure state.

Allocates space for a state-vector of complex amplitudes, which assuming a single qreal floating-point number requires qrealBytes, requires memory

$\text{qrealBytes} \times 2 \times 2^\text{numQubits}\;\;\text{(bytes)},$

though there are additional memory costs in GPU and distributed modes.

The returned Qureg begins in the zero state, as produced by initZeroState().

Once created, the following Qureg fields are relevant in all backends:

QuESTEnv env must be prior created with createQuESTEnv().

Serial

In serial and local (non-distributed) multithreaded modes, a state-vector Qureg costs only the memory above. For example, at double precision (QuEST_PREC = 2, qrealBytes = 8), the memory costs are:

`numQubits`	memory
10	16 KiB
16	1 MiB
20	16 MiB
26	1 GiB
30	16 GiB

Individual amplitudes should be fetched and modified with functions like getAmp() and setAmps(). However, it is sometimes useful to access the state-vector directly, for example to create your own low-level (high performance) multithreaded functions. In those instants, Qureg.stateVec can be accessed directly, storing the real and imaginary components of the state-vector amplitudes in:

Qureg.stateVec.real
Qureg.stateVec.imag

The total number of amplitudes in the state-vector is

Qureg.numAmpsTotal

For example,

Qureg qureg = createQureg(10, env);
 
// ruin a perfectly good state-vector
for (long long int i=0; i<qureg.numAmpsTotal; i++) {
    qureg.stateVec.real[i] = rand();
    qureg.stateVec.imag[i] = rand(); 
}

GPU

In GPU-accelerated mode, an additional state-vector is created in GPU memory. Therefore both RAM and VRAM must be of sufficient memory to store the state-vector, each of the size indicated in the Serial table above.

Note that many GPUs do not support quad precision qreal.

Individual amplitudes of the created Qureg should be fetched and modified with functions like getAmp() and setAmps(). This is especially important since the GPU state-vector can be accessed directly, and changes to Qureg.stateVec will be ignored and overwritten. To modify the state-vector "directly", one must use copyStateFromGPU() and copyStateToGPU() before and after.

For example,

Qureg qureg = createQureg(10, env);
 
// ruin a perfectly good state-vector
for (long long int i=0; i<qureg.numAmpsTotal; i++) {
    qureg.stateVec.real[i] = rand();
    qureg.stateVec.imag[i] = rand(); 
}
copyStateToGPU();

Distributed

In distributed mode, the state-vector is uniformly partitioned between the N distributed nodes.

Only a power-of-2 number of nodes N may be used (e.g. N = 1, 2, 4, 8, ...). There must additionally be at least 1 amplitude of a state-vector stored on each node. This means one cannot create a state-vector Qureg with fewer than $\log_2(\text{N})$ qubits.

In addition to Qureg.stateVec, additional memory is allocated on each node for communication buffers, of size equal to the state-vector partition. Hence the total memory per-node required is:

$2 \times \text{qrealBytes} \times 2 \times 2^\text{numQubits}/N \;\;\text{(bytes)},$

For example, at double precision (QuEST_PREC = 2, qrealBytes = 8), the memory costs are:

`numQubits`	memory per node
	N = 2	N = 4	N = 8	N = 16	N = 32
10	16 KiB	8 KiB	4 KiB	2 KiB	1 KiB
20	16 MiB	8 MiB	4 MiB	2 MiB	1 MiB
30	16 GiB	8 GiB	4 GiB	2 GiB	1 GiB
40	16 TiB	8 TiB	4 TiB	2 TiB	1 TiB

State-vector amplitudes should be set and modified using getAmp() and setAmps(). Direct modification is possible, but should be done extremely carefully, since each node only stores a partition of the full state-vector, which itself mightn't fit on any single node. Furthermore, an asynchronous MPI process may may unexpectedly modify local amplitudes; avoid this with syncQuESTEnv().

The fields relevant to distribution are:

Qureg.numAmpsPerChunk: the length of Qureg.stateVec (.real and .imag) on each node.
Qureg.chunkId: the id of the node, from 0 to N-1.

Therefore, this code is valid

syncQuESTEnv(env);
// set state |i> to have amplitude i
for (long long int i=0; i<qureg.numAmpsPerChunk; i++)
    qureg.stateVec.real[i] = i + qureg.chunkId * qureg.numAmpsPerChunk;

while the following erroneous code would cause a segmentation fault:

// incorrectly attempt to set state |i> to have amplitude i
for (long long int i=0; i<qureg.numAmpsTotal; i++)
    qureg.stateVec.real[i] = i;

See also

createDensityQureg() to create a density matrix of the equivalent number of qubits, which can enter noisy states.
createCloneQureg() to create a new qureg of the size and state of an existing qureg.
destroyQureg() to free the allocated Qureg memory.
reportQuregParams() to print information about a Qureg.
copyStateFromGPU() and copyStateToGPU() for directly modifying state-vectors in GPU mode.
syncQuESTEnv() for directly modifying state-vectors in distributed mode.

Returns: an object representing the set of qubits

Parameters

[in]	numQubits	number of qubits in the system
[in]	env	object representing the execution environment (local, multinode etc)

Exceptions

invalidQuESTInputError()	if `numQubits` <= 0 if `numQubits` is so large that the number of amplitudes cannot fit in a long long int type, if in distributed mode, there are more nodes than elements in the would-be state-vector
exit	if in GPU mode, but GPU memory cannot be allocated.

Author: Ania Brown; Tyson Jones (validation, doc)

Definition at line 36 of file QuEST.c.

                                                {
     validateNumQubitsInQureg(numQubits, env.numRanks, __func__);
     
     Qureg qureg;
     statevec_createQureg(&qureg, numQubits, env);
     qureg.isDensityMatrix = 0;
     qureg.numQubitsRepresented = numQubits;
     qureg.numQubitsInStateVec = numQubits;
     
     qasm_setup(&qureg);
     initZeroState(qureg); // safe call to public function
     return qureg;
 }

References initZeroState(), Qureg::isDensityMatrix, Qureg::numQubitsInStateVec, Qureg::numQubitsRepresented, QuESTEnv::numRanks, qasm_setup(), statevec_createQureg(), and validateNumQubitsInQureg().

Referenced by TEST_CASE().

◆ destroyComplexMatrixN()

void destroyComplexMatrixN ( ComplexMatrixN matr )

Destroy a ComplexMatrixN instance created with createComplexMatrixN()

It is invalid to attempt to destroy a matrix created with getStaticComplexMatrixN().

See also

Parameters

[in] matr the dynamic matrix (created with createComplexMatrixN()) to deallocate

Exceptions

invalidQuESTInputError()	if `matr` was not yet allocated.
malloc_error	if `matr` was static (created with getStaticComplexMatrixN())

Author: Tyson Jones

Definition at line 1369 of file QuEST.c.

                                              {
     /* this checks m.real/imag != NULL, which is only ever set when the mallocs 
      * in createComplexMatrixN fail, which already prompts an error. Hence 
      * this check if useless 
      */
     validateMatrixInit(m, __func__);
     
     int numRows = 1 << m.numQubits;
     for (int r=0; r < numRows; r++) {
         free(m.real[r]);
         free(m.imag[r]);
     }
     free(m.real);
     free(m.imag);
 }

References ComplexMatrixN::imag, ComplexMatrixN::numQubits, ComplexMatrixN::real, and validateMatrixInit().

Referenced by densmatr_mixMultiQubitKrausMap(), densmatr_mixTwoQubitKrausMap(), and TEST_CASE().

◆ destroyDiagonalOp()

void destroyDiagonalOp	(	DiagonalOp	op,
		QuESTEnv	env
	)

Destroys a DiagonalOp created with createDiagonalOp(), freeing its memory.

See also

createDiagonalOp()

Parameters

[in]	op	the DiagonalOp to destroy
[in]	env	the QuESTEnv

Exceptions

invalidQuESTInputError()

if op was not previously created

Author: Tyson Jones

Definition at line 1524 of file QuEST.c.

                                                     {
     // env accepted for API consistency
     validateDiagOpInit(op, __func__);
     
     agnostic_destroyDiagonalOp(op);
 }

References agnostic_destroyDiagonalOp(), and validateDiagOpInit().

Referenced by TEST_CASE().

◆ destroyPauliHamil()

void destroyPauliHamil ( PauliHamil hamil )

Destroy a PauliHamil instance, created with either createPauliHamil() or createPauliHamilFromFile().

Parameters

[in] hamil a dynamic PauliHamil instantiation

Author: Tyson Jones

Definition at line 1414 of file QuEST.c.

                                      {
     
     free(h.termCoeffs);
     free(h.pauliCodes);
 }

References PauliHamil::pauliCodes, and PauliHamil::termCoeffs.

Referenced by createDiagonalOpFromPauliHamilFile(), TEST_CASE(), validateDiagPauliHamilFromFile(), validateHamilFileCoeffParsed(), validateHamilFilePauliCode(), and validateHamilFilePauliParsed().

◆ destroyQuESTEnv()

void destroyQuESTEnv ( QuESTEnv env )

Destroy the QuEST environment.

If something needs to be done to clean up the execution environment, such as finalizing MPI when running in distributed mode, it is handled here

See also

createQuESTEnv()

Parameters

[in] env object representing the execution environment. A single instance is used for each program

Author: Ania Brown

Definition at line 174 of file QuEST_cpu_distributed.c.

                                   {
     free(env.seeds);
     
     int finalized;
     MPI_Finalized(&finalized);
     if (!finalized) MPI_Finalize();
     else printf("ERROR: Trying to close QuESTEnv multiple times. Ignoring\n");
 }

References QuESTEnv::seeds.

Referenced by main().

◆ destroyQureg()

void destroyQureg	(	Qureg	qureg,
		QuESTEnv	env
	)

Deallocate a Qureg, freeing its memory.

This frees all memory bound to qureg, including its state-vector or density matrix in RAM, in VRAM (in GPU mode), and communication buffers (in distributed mode).

The qureg must have been previously created with createQureg(), createDensityQureg() or createCloneQureg().

See also

Parameters

[in,out]	qureg	the Qureg to be destroyed
[in]	env	the QuESTEnv

Author: Ania Brown; Tyson Jones (improved doc)

Definition at line 77 of file QuEST.c.

                                              {
     statevec_destroyQureg(qureg, env);
     qasm_free(qureg);
 }

References qasm_free(), and statevec_destroyQureg().

Referenced by TEST_CASE().

◆ initComplexMatrixN()

void initComplexMatrixN	(	ComplexMatrixN	m,
		qreal	real[][1<< m.numQubits],
		qreal	imag[][1<< m.numQubits]
	)

Initialises a ComplexMatrixN instance to have the passed real and imag values.

This allows succint population of any-sized ComplexMatrixN, e.g. through 2D arrays:

ComplexMatrixN m = createComplexMatrixN(3);
initComplexMatrixN(m, 
    (qreal[8][8]) {{1,2,3,4,5,6,7,8}, {0}},
    (qreal[8][8]) {{0}});

m can be created by either createComplexMatrixN() or getStaticComplexMatrixN().

This function is only callable in C, since C++ signatures cannot contain variable-length 2D arrays

Parameters

[in]	m	the matrix to initialise
[in]	real	matrix of real values; can be 2D array of array of pointers
[in]	imag	matrix of imaginary values; can be 2D array of array of pointers

Exceptions

invalidQuESTInputError()

if m has not been allocated (e.g. with createComplexMatrixN())

Author: Tyson Jones

Definition at line 1386 of file QuEST.c.

                                                                                                   {
     validateMatrixInit(m, __func__);
     
     int dim = 1 << m.numQubits;
     for (int i=0; i<dim; i++)
         for (int j=0; j<dim; j++) {
             m.real[i][j] = re[i][j];
             m.imag[i][j] = im[i][j];
         }
 }

References ComplexMatrixN::imag, ComplexMatrixN::numQubits, ComplexMatrixN::real, and validateMatrixInit().

◆ initDiagonalOp()

void initDiagonalOp	(	DiagonalOp	op,
		qreal *	real,
		qreal *	imag
	)

Overwrites the entire DiagonalOp op with the given real and imag complex elements.

Both real and imag must have length equal to pow(2, op.numQubits).

In GPU mode, this updates both the RAM (op.real and op.imag) and persistent GPU memory; there is no need to call syncDiagonalOp() afterward.

In distributed mode, this function assumes real and imag exist fully on every node. For DiagonalOp which are too large to fit into a single node, use setDiagonalOpElems() or syncDiagonalOp().

See also

Parameters

[in,out]	op	the diagonal operator to modify
[in]	real	the real components of the full set of new elements
[in]	imag	the imaginary components of the full set of new elements

Exceptions

invalidQuESTInputError()	if `op` was not created
segmentation-fault	if either `real` or `imag` have length smaller than pow(2, `op.numQubits`)

Author: Tyson Jones

Definition at line 1537 of file QuEST.c.

                                                              {
     validateDiagOpInit(op, __func__);
     
     agnostic_setDiagonalOpElems(op, 0, real, imag, 1LL << op.numQubits);
 }

References agnostic_setDiagonalOpElems(), DiagonalOp::numQubits, and validateDiagOpInit().

Referenced by TEST_CASE().

◆ initDiagonalOpFromPauliHamil()

void initDiagonalOpFromPauliHamil	(	DiagonalOp	op,
		PauliHamil	hamil
	)

Populates the diagonal operator op to be equivalent to the given Pauli Hamiltonian hamil, assuming hamil contains only PAULI_Z operators.

Given a PauliHamil hamil featuring only PAULI_Z and PAULI_I, with term coefficients 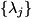$\{\lambda_j\}$ , which hence has form

$\begin{aligned} \text{hamil} &= \sum\limits_j^{\text{numSumTerms}} \lambda_j \bigotimes\limits_{k_j} \hat{Z}_k \\ &\equiv \begin{pmatrix} r_1 \\ & r_2 \\ & & r_3 \\ & & & \ddots \\ & & & & r_{2^{\,\text{numQubits}}} \end{pmatrix}, \end{aligned}$

this function modifies op to

$\text{op} \; \rightarrow \; \text{diag} \big( \; r_1, \; r_2, \; r_3, \; \dots, \; r_{2^{\,\text{numQubits}}} \, \big),$

where the real amplitudes have form

$r_i = \sum\limits_j \, s_{ij} \, \lambda_j, \;\;\;\; s_{ij} = \pm 1 \,.$

This is useful since calculations with DiagonalOp are significantly faster than the equivalent calculations with a general PauliHamil. For example, applyDiagonalOp() requires a factor numSumTerms * numQubits fewer operations than applyPauliHamil().

In distributed mode, each node will contain only a sub-partition of the full diagonal matrix.
In GPU mode, both the CPU and GPU memory copies of op will be updated, so there is no need to call syncDiagonalOp() afterward.

See also

Parameters

[in,out]	op	an existing DiagonalOp (e.g. created with createDiagonalOp()) to modify
[in]	hamil	a PauliHamil of equal dimension to `op`, containing only `PAULI_Z` and `PAULI_I` operators

Exceptions

invalidQuESTInputError()	if `hamil` has invalid parameters (`numQubits` <= 0, `numSumTerms` <= 0) if `op` and `hamil` have unequal dimensions if `hamil` contains any operator other than `PAULI_Z` and `PAULI_I`
segmentation-fault	if either `op` or `hamil` have not been already created

Author: Tyson Jones; Milos Prokop (serial prototype)

Definition at line 1550 of file QuEST.c.

                                                                    {
     validateHamilParams(hamil.numQubits, hamil.numSumTerms, __func__);
     validateDiagOpInit(op, __func__);
     validateDiagPauliHamil(op, hamil, __func__);
     
     agnostic_initDiagonalOpFromPauliHamil(op, hamil);
 }

References agnostic_initDiagonalOpFromPauliHamil(), PauliHamil::numQubits, PauliHamil::numSumTerms, validateDiagOpInit(), validateDiagPauliHamil(), and validateHamilParams().

Referenced by TEST_CASE().

◆ initPauliHamil()

void initPauliHamil	(	PauliHamil	hamil,
		qreal *	coeffs,
		enum pauliOpType *	codes
	)

Initialise PauliHamil instance hamil with the given term coefficients and Pauli codes (one for every qubit in every term).

Arguments coeffs and codes encode a weighted sum of Pauli operators, with the same format as other QuEST functions (like calcExpecPauliSum()).

This is useful to set the elements of the PauliHamil in batch.
For example

int numQubits = 3;
int numTerms = 2;
PauliHamil hamil = createPauliHamil(numQubits, numTerms);
 
// hamil = 0.5 X0 Y1 - 0.5 Z1 X3
initPauliHamil(hamil, 
    (qreal[]) {0.5, -0.5}, 
    (enum pauliOpType[]) {PAULI_X,PAULI_Y,PAULI_I, PAULI_I, PAULI_Z, PAULI_X});

The initialised PauliHamil can be previewed with reportPauliHamil().

hamil must be already created with createPauliHamil(), or createPauliHamilFromFile().

See also

Parameters

[in,out]	hamil	an existing PauliHamil instance to be modified
[in]	coeffs	an array of sum term coefficients, which must have length `hamil.numSumTerms`
[in]	codes	a flat array of Pauli codes, of length `hamil.numSumTerms`*`hamil.numQubits`

Exceptions

invalidQuESTInputError()

if hamil has invalid parameters (numQubits <= 0, numSumTerms <= 0)
if any code in codes is not a valid Pauli code (pauliOpType)

Author: Tyson Jones

Definition at line 1504 of file QuEST.c.

                                                                               {
     validateHamilParams(hamil.numQubits, hamil.numSumTerms, __func__);
     validatePauliCodes(codes, hamil.numSumTerms*hamil.numQubits, __func__);
     
     int i=0;
     for (int t=0; t<hamil.numSumTerms; t++) {
         hamil.termCoeffs[t] = coeffs[t];
         for (int q=0; q<hamil.numQubits; q++) {
             hamil.pauliCodes[i] = codes[i];
             i++;
         }
     }
 }

References PauliHamil::numQubits, PauliHamil::numSumTerms, PauliHamil::pauliCodes, PauliHamil::termCoeffs, validateHamilParams(), and validatePauliCodes().

Referenced by TEST_CASE().

◆ setDiagonalOpElems()

void setDiagonalOpElems	(	DiagonalOp	op,
		long long int	startInd,
		qreal *	real,
		qreal *	imag,
		long long int	numElems
	)

Modifies a subset (starting at index startInd, and ending at index startInd + numElems) of the elements in DiagonalOp op with the given complex numbers (passed as real and imag components).

In GPU mode, this updates both the RAM (op.real and op.imag), and the persistent GPU memory.

In distributed mode, this function assumes the subset real and imag exist (at least) on the node containing the ultimately updated elements.
For example, below is the correct way to modify the full 8 elements of op when split between 2 nodes.

DiagonalOp op = createDiagonalOp(3, env);
 
int numElems = 4;
qreal re[] = {1,2,3,4};
qreal im[] = {1,2,3,4};
setDiagonalOpElems(op, 0, re, im, numElems);
 
// modify re and im to the next set of elements 
for (int i=0; i<4; i++) {
  re[i] += 4;
  im[i] += 4;
}
setDiagonalOpElems(op, 4, re, im, numElems);

In this way, one can avoid a single node containing all new elements which might not fit. If more elements are passed than exist on an individual node, each node merely ignores the additional elements.

Parameters

[in,out]	op	the DiagonalOp to modify
[in]	startInd	the starting index (globally) of the subset of elements to modify
[in]	real	the real components of the new elements
[in]	imag	the imaginary components of the new elements
[in]	numElems	the number of new elements (the length of `real` and `imag`)

Exceptions

invalidQuESTInputError()	if `op` was not created if `startInd` is an invalid index (<0 or >=pow(2,`op.numQubits`)) if `numElems` is an invalid number of elements (<=0 or >pow(2,`op.numQubits`)) if there are fewer than `numElems` elements in `op` after `startInd`
segmentation-fault	if either `real` or `imag` have fewer elements than `numElems`

Author: Tyson Jones

Definition at line 1543 of file QuEST.c.

                                                                                                                  {
     validateDiagOpInit(op, __func__);
     validateNumElems(op, startInd, numElems, __func__);
     
     agnostic_setDiagonalOpElems(op, startInd, real, imag, numElems);
 }

References agnostic_setDiagonalOpElems(), validateDiagOpInit(), and validateNumElems().

Referenced by TEST_CASE().

◆ syncDiagonalOp()

void syncDiagonalOp ( DiagonalOp op )

Update the GPU memory with the current values in op.real and op.imag.

This is required after making manual changes to op, but is not required after functions initDiagonalOp() and setDiagonalOpElems().

This function has no effect in other modes besides GPU mode.

See also

Parameters

[in,out] op the DiagonalOp to synch to GPU

Exceptions

invalidQuESTInputError()

if op was not created

Author: Tyson Jones

Definition at line 1531 of file QuEST.c.

                                    {
     validateDiagOpInit(op, __func__);
     
     agnostic_syncDiagonalOp(op);
 }

References agnostic_syncDiagonalOp(), and validateDiagOpInit().

Referenced by TEST_CASE().

Data Structures

Macros

Enumerations

Functions

Detailed Description

Macro Definition Documentation

◆ fromComplex

◆ getStaticComplexMatrixN

◆ qcomp

◆ qreal

◆ QuEST_PREC

◆ toComplex

Enumeration Type Documentation

◆ bitEncoding

◆ pauliOpType

◆ phaseFunc

Function Documentation

◆ createCloneQureg()

◆ createComplexMatrixN()

◆ createDensityQureg()

Serial

GPU

Distributed

◆ createDiagonalOp()

GPU

Distribution

◆ createDiagonalOpFromPauliHamilFile()

◆ createPauliHamil()

◆ createPauliHamilFromFile()

◆ createQuESTEnv()

◆ createQureg()

Serial

GPU

Distributed

◆ destroyComplexMatrixN()

◆ destroyDiagonalOp()

◆ destroyPauliHamil()

◆ destroyQuESTEnv()

◆ destroyQureg()

◆ initComplexMatrixN()

◆ initDiagonalOp()

◆ initDiagonalOpFromPauliHamil()

◆ initPauliHamil()

◆ setDiagonalOpElems()

◆ syncDiagonalOp()